VOLVER A LOS ARTÍCULOS
Se definen como la inversa de la función exponencial. Tienen múltiples usos y resultan fáciles de calcular gracias a las nuevas calculadoras.
La idea de logaritmo comenzó a desarrollarse hacia el sigo XV para facilitar la labor de profesionales de la astronomía y economía. El objetivo era simplificar las engorrosas multiplicaciones, divisiones y raíces de números con muchas cifras.
Algunos sostienen que el matemático y relojero Jobst Bürgi inventó los logaritmos a principios del siglo XVI. Sin embargo, los créditos se los suele llevar el escocés John Napier quien publicó en 1614 su obra “Mirifici logaithmorum canonis descriptio” (descripción de la maravillosa regla de los logaritmos) con las primeras tablas de logaritmos para el seno y el coseno de un ángulo a intervalos de 1’ y con siete cifras.
En aquella época para obtener el resultado de los logaritmos se hacían cuentas complejas y los resultados se registraban en tablas. De este modo, se facilitó posteriormente la resolución de los logaritmos, pues solo bastó con aprender a ver los resultados en la tabla.
Las primeras tablas fueron confeccionadas por Henry Briggs y tenían una precisión de 10 cifras decimales. Con la invención de las calculadoras científicas, las famosas tablas quedaron en la historia y ahora con tan solo presionar un par de botones se puede llegar fácilmente al resultado.
Como podemos ver, los logaritmos no son un invento del siglo XXI sino que existen y se utilizan desde hace cientos de años. Pero, ¿qué son las funciones logarítmicas?
Una función logarítmica es aquella que genéricamente se expresa como f(x) = logax, siendo “a” la base de esta función, que ha de ser positiva y distinta de 1.
La función logarítmica es la inversa de la función exponencial, dado que:
loga x = b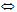 
ab = x.
Esto quiere decir que el logaritmo de “x” en base “a” es igual a “b”. Esta función es equivalente a “a” elevado a la “b” que da como resultado “x”.
Razonemos esto con números:
¿A qué exponente hay que elevar la base 5 para obtener 25?
Al exponente 2, ya que 52 = 25.
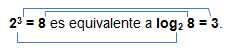
Decimos que “el logaritmo de 25 en la base 5 es 2”, es decir, log5 25 = 2
Entonces, log5 25 = 2 es equivalente a 52 = 25.
Te recomendamos que releas estás últimas cuatro líneas nuevamente, considerando que un logaritmo es un exponente.
Decimales y Neperianos
log 10 = log 101 = 1
log 100 = log 102 = 2
log 1000 = log 103 = 3
log 10000 = log 104= 4
Por otra parte:
log 0,1 = log 10-1 = -1
log 0,01 = log 10-2 = -2
log 0,001 = log 10-3 = -3
Propiedades elementales
1) loga a = 1
2) loga 1 = 0
3) loga ax = x
¿Para qué se usan los logaritmos?
Por ejemplo, la escala de Richter es logarítmica. Fue creada en 1935 por el sismólogo estadounidense Charles Richter con la colaboración de Beno Gutenberg bajo el objetivo de cuantificar la energía liberada en un terremoto. Optaron por incorporar el logaritmo ya que permite que los valores asignados a cada nivel aumenten de forma logarítmica, y no de forma lineal. Richter tomó la idea del uso de logaritmos en la escala de magnitud estelar, usada en la astronomía para describir el brillo de las estrellas y de otros objetos celestes.
Otro ejemplo de escala logarítmica es el pentagrama utilizado en Occidente para escribir música: la diferencia en la altura del sonido es proporcional al logaritmo de la frecuencia.
Los astrónomos para determinar la magnitud de un planeta o la estelar de una estrella utilizan los logaritmos.
Los logaritmos fueron desarrollados mucho antes que las computadoras, por lo que antiguamente se los utilizaba a diario para simplificar el cálculo. Cuando se trabajaba con números muy grandes o muy pequeños, se recurría a ellos. Resultaban tan importantes que se destinaba mucho tiempo a su análisis, así nacieron las propiedades que simplificaron mucho más el cálculo. Actualmente se utilizan las calculadoras o las computadoras, pero para encontrar explicación a ciertos temas, se siguen usando los logaritmos.
Calculadora científica. Permite resolver funciones logarítmicas.
