Porcentajes

---

Solo por hoy 30% de descuento en productos seleccionados.
El 40% de los damnificados aún no recibieron ayuda.
Los sueldos aumentarán un 20%.
El 30% de la población mundial tiene acceso a Internet.

¿Algunas de las expresiones anteriores te resultan conocidas? En cada una de ellas se habla de porcentaje (%), es una forma de referirse a una parte del todo. El porcentaje representa a una fracción decimal cuyo denominador es 100.

Analicemos lo siguiente: el 30% de la población mundial tiene acceso a Internet.

30 Numerador. Representa a una parte del todo.
-----
100 Denominador. Representa al todo, en este ejemplo sería a la población mundial.

El entero tiene el valor 100 y lo indicamos escribiéndolo como 100%, es decir, el entero es igual al cien por ciento.

El 30% equivale a 30/100, que si buscamos una fracción equivalente simplificada es igual a 3/10, que a su vez es igual a 0,3 (3: 10 = 0,3)

Veamos otro ejemplo para comprender los porcentajes.

Imaginemos una sala de cine. En total hay 100 espectadores, de los cuales 20 usan anteojos. La fracción decimal correspondiente es 20/100. El resto de los espectadores 80/100 no utiliza anteojos.

Ahora vamos a representar estas cantidades utilizando porcentajes.

Espectadores que usan anteojos ---------- 20/100 20%

Espectadores que no usan anteojos ------ 80/100 80%

La expresión que vemos arriba se lee así:

El veinte por ciento (20%) de los espectadores usa anteojos, mientras que el ochenta por ciento (80%) no usa anteojos.

Los porcentajes se utilizan diariamente para representar estadísticas, descuentos o recargos en compras. Los científicos los usan para expresar concentraciones, etc.

CALCULAR PORCENTAJES

En la vida cotidiana nos encontraremos con situaciones donde tendremos que calcular porcentajes de una cantidad determinada. Por ejemplo, al acercarnos a una vidriera donde se indica que hay 20% de descuento en ciertos productos, necesitaremos calcular el valor actual de cada producto ya que habitualmente se exhibe el precio viejo para que los clientes sean conscientes del descuento. Así, tendremos que saber cuánto es el 30% de $120, por ejemplo.

A continuación veremos dos métodos para calcular porcentajes.

Método 1: pensaremos al porcentaje como una fracción decimal. De esta manera, si queremos calcular el 30% de 120 debemos hacer lo siguiente.

Transformamos el porcentaje en una fracción decimal.

30% = 30/100

Luego multiplicamos esta fracción por el valor que representa al total (120)

30/100. 120 = 36

Una manera de resolver esta cuenta es considerando que una fracción es una división, entonces, primero hay que hacer 30 dividido 100 y, luego al resultado, multiplicarlo por 120.

Como respuesta decimos: el 30% de 120 es 36

Resumiendo, al resolver de esta forma transformamos el porcentaje “%” a una fracción decimal con denominador 100 y el “de” por una multiplicación. De acuerdo al ejemplo anterior:

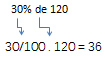
Por último damos la respuesta final: el 30% de 120 es 36. El descuento sería de $36 pesos. $120 - $36 = $84

Método 2: utilizaremos la regla de tres simple para resolver los porcentajes teniendo en cuenta que al trabajar con porcentajes estamos trabajando con cantidades directamente proporcionales, por lo tanto la regla de tres simple será directa. Para mostrar cómo se resuelve utilizando esta forma, calcularemos el 15% de 80, suponiendo que una bufanda cuesta $80 pero que nos recargan el 15% por pagar con tarjeta de crédito. ¿Cuánto tenemos que pagar por la bufanda?

Plantearemos:

100% ----------- $80

15% ------------- X

Partimos de saber que el 100% (el total) es $80, luego ¿Qué cantidad le corresponde al 15%? A esta incógnita la indicamos con la letra X.

Resolvemos la regla de tres, obteniendo el valor de nuestra incógnita (X).

X = (15 . 80) : 100

X = 12

Respuesta: El 15% de $80 es $12. Por lo tanto a $80 le tenemos que sumar $12, que es igual a $92.