 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS

Una desigualdad es una expresión matemática que contiene un signo que expresa que dos valores no son iguales. Los signos de desigualdad son: ≠ < > ≤ ≥

Una desigualdad es similar a una ecuación. Hay dos expresiones separadas por un símbolo que indica la relación que tiene cada una de las partes. En una ecuación tal como 7x = 49, el signo igual (=) indica que las expresiones son equivalentes. En una desigualdad, tal como 57 > 49, el signo > (mayor) indica que el lado izquierdo es mayor que el lado derecho.
Los símbolos de desigualdad que se utilizan en matemáticas son:
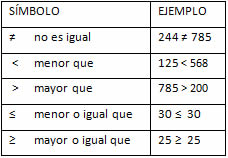
Propiedades de las desigualdades
1. Si a los dos miembros de una desigualdad se les suma o resta un mismo número o una expresión algebraica se obtiene otra desigualdad del mismo sentido.

Ejemplo:

2. Si los dos miembros de una desigualdad se multiplican o dividen por un número positivo, su sentido no varía.
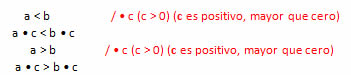
Ejemplo:

3. Si los dos miembros de una desigualdad se multiplican o dividen por un número negativo, se obtiene otra desigualdad de sentido contrario. El sentido varía.
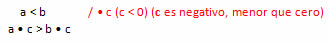

Ejemplo:

De manera recíproca, cuando la parte de la incógnita resulta negativa, deben invertirse los signos a ambos lados y cambiar el sentido de la desigualdad, ya que no puede haber desigualdades con incógnita negativa.
Inecuaciones de primer grado con una incógnita
Una inecuación es una desigualdad en la que aparece alguna incógnita en uno o en los dos miembros de una desigualdad.
Ejemplos: 2 + 4x < 6 x2 – 5x + 2 ≥ 0 4x – y > 5y + 3x – 13
Las inecuaciones se clasifican por el grado y las incógnitas que tiene.
Para comprenderlo, los desafiamos a resolver el siguiente planteo:
Encontrar los números que verifican: que el doble menos uno sea mayor que si al número le sumamos 4.
Algebraicamente se expresaría así:
2 x – 1 > x + 4
Como se puede verificar, existen muchos números que cumplen con la inecuación. Ejemplo: el 9, el 11… Y también se pueden encontrar números que no coinciden con la inecuación. Ejemplo: el 3, el -4…
Conclusión: una inecuación no tiene una única solución como las ecuaciones.
Se puede afirmar que, en general, una inecuación tiene infinitas soluciones.
Resolvamos la anterior inecuación, aplicando las propiedades de las desigualdades.
Sumamos 1 a los dos miembros 2x > x + 4 + 1
Restamos x a los dos miembros 2x – x > 4 + 1
Reducimos miembros x > 5
Por tanto, la solución de esta inecuación es: x > 5
Las soluciones de una inecuación son los valores que puede tomar la incógnita tales que al sustituirlos en la inecuación la conviertan en una desigualdad cierta.
Inecuación: 2 x – 1 > x + 4 si sustituimos la x por 7
2 • 7 – 1 > 7 + 4
14 > 11 que es una desigualdad cierta, y, por tanto, el valor 7 será una solución.
2 • 2 – 1 > 2 + 4
4 > 6 no es cierta la desigualdad, por tanto, el valor 2 no es solución.
* Para resolver una inecuación se transforma en otras más sencillas que sean equivalentes.
* Dos inecuaciones son equivalentes cuando ambas tienen las mismas soluciones.
Las propiedades que permiten transformar inecuaciones en otras más sencillas son las mismas que las propiedades de las desigualdades, simplemente cambiando la palabra desigualdad por inecuación.