VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
DEFINICIÓN DE NÚMERO COMPLEJO:
Un número complejo Z, se define mediante la expresión:
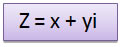
También puedes encontrarlo expresado de estas formas:
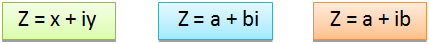
En este artículo utilizaremos la forma Z = x + yi.
Siendo x e y números reales.
x: parte real
y: parte imaginaria
A la expresión x + yi se la denomina FORMA BINÓMICA de un número complejo.
Teniendo en cuenta esta definición, podemos decir que un número real está incluido en el conjunto de los números complejos; ya que un número complejo cuya parte imaginaria es cero, estaría compuesto solo por un número real. Veamos dos ejemplos para aclarar este concepto:

OPERACIONES CON NÚMEROS COMPLEJOS EN FORMA BINÓMICA:
Antes de estudiar las operaciones con números complejos en forma binómica, debes saber lo siguiente:
OPUESTO DE UN NÚMERO COMPLEJO: El opuesto de un número complejo Z se nota -Z.
El opuesto del número Z = x+yi es:
-Z=-x-yi
Para todo número x e y pertenecientes a reales.
CONJUGADO DE UN NÚMERO COMPLEJO: El conjugado de un número complejo Z=x+yi, es:
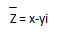
SUMA:
Z1 = x1 + y1i ^ Z2 = x2 + y2i
Z1 + Z2 = (x1 + x2) + (y1 + y2) i
Ejemplo:
Z1 = 3 + 5i ^ Z2 = 2 - 4i
Z1 + Z2 = (3 + 2) + (5 - 4) i
Z1 + Z2 = 5 + 1 i
Z1 + Z2 = 5 + i
RESTA:
Z1 = x1 + y1i ^ Z2 = x2 + y2 i
Z1 - Z2 = (x1 - x2) + (y1 - y2) i
Ejemplo:
Z1 = 3 + 5i ^ Z2 = 2 - 4i
Z1 - Z2 = (3 - 2) + [5 - (-4)] i
Z1 - Z2 = 1 + 9 i
Z1 - Z2 = 1 +9i
PRODUCTO:
Z1 = x1 +y1i ^ Z2 = x2 +y2i
Z1 . Z2 = (x1 + y1i) (x2 + y2i) Se realiza propiedad distributiva.
Z1.Z2 = x1 . x2 + x1 . y2i + y1i. x2 + y1i. y2i
Ejemplo:
Z1 = 3 + 5i ^ Z2 = 2 - 4i
Z1 . Z2 =(3 + 5i) (2 - 4i)
Z1 . Z2 = 3. 2 + 3.(-4i) + 5i. 2 + 5i . (-4i)
Z1 . Z2 = 6 - 12i + 10i - 20 i2
Z1 . Z2 = 6 - 12i + 10i - 20 (-1)
Z1 . Z2 = 6 - 12i + 10i + 20
Z1 . Z2 = 26 - 2i
COCIENTE:
Z1 = x1 + y1i ^ Z2 = x2 + y2 i
Z1 : Z2 = (x1 + y1i) : ( x2 + y2i)
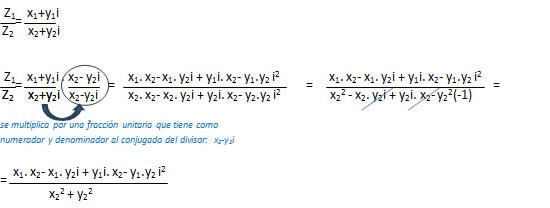
Veamos un ejemplo:
Z1 = 2 + 5i ^ Z2 = -3 + 4i
Z1 :Z2 = (2 + 5i) : (-3 + 4i)