VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
En estos sistemas, cada cifra del numeral tiene un valor posicional; es decir, ocupa una ubicación específica
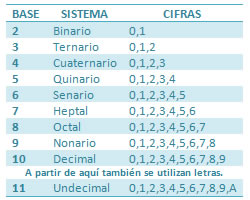
La cantidad de símbolos permitidos en cada uno de estos sistemas depende de la base del mismo. Por ejemplo:

SISTEMA DECIMAL: Este sistema utiliza como base el 10, cada cifra adquiere un valor relativo de acuerdo a la posición en que se encuentre.
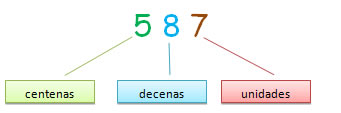
Como se observa en el ejemplo, el número quinientos ochenta y siete, está formado por 5 centenas, 8 decenas y 7 unidades.
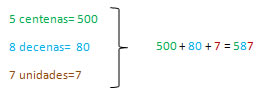
Si expresamos este numeral como una descomposición polinómica, obtendremos:
587 = 5.102 + 8.101 + 7.100
La descomposición polinómica consiste en multiplicar a cada cifra por diez elevado a la potencia correspondiente según su posición.
unidades: . 100
decenas: . 101
centenas: . 102
unidades de mil: . 103
Y así sucesivamente.
Si continuamos resolviendo:
587 = 5 . 102 + 8 . 101 + 7 . 100
587 = 5 . 100 + 8 . 10 + 7 . 1
Podemos decir que:
587 = 500 + 80 + 7
SISTEMA BINARIO: En este sistema solamente se utilizan el 0 y el 1 para representar los números.
¿Cómo transformar al número decimal 20 al sistema binario?
El procedimiento es el siguiente:
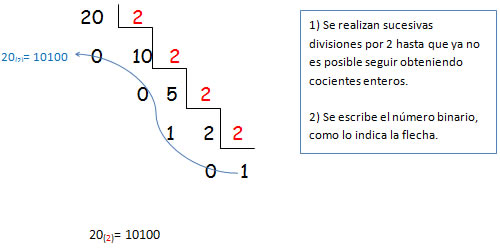
Comprobamos:
10100 = 1.24 + 0 . 23 + 1 . 22 + 0 . 21 + 0 . 20 = 16 + 4 = 20
Como es sistema binario, se multiplica cada cifra por 2 elevado a la potencia que corresponda a su posición.
El mismo procedimiento se puede realizar para transformar un número decimal a un sistema con otra base. Veamos un ejemplo más:
Convertir a sistema senario el número decimal 624:
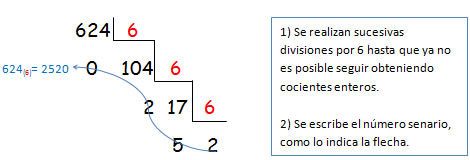
Comprobamos:
2520 = 2 . 63 + 5 . 62 + 2 . 61 + 0 . 60 = 2 . 216 + 5 . 36 + 2 . 6 + 0 . 6 = 432 + 180 + 12 = 624
PARA RECORDAR: