VOLVER A LOS ARTÍCULOS
La trigonometría es el estudio de las relaciones entre los lados y los ángulos de un triángulo. Los egipcios utilizaron estos conocimientos para la construcción de las pirámides. Más tarde Euler (1707-1783), instauró la trigonometría moderna, estableciendo la notación actual de las funciones trigonométricas.
1. Antes de ver cuáles son las razones trigonométricas, veremos al protagonista de la trigonometría, el triángulo rectángulo.
2. Datos que no puedes dejar de saber
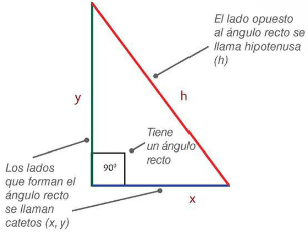
Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90°; y la suma de todos sus ángulos es de 180°.
En un triángulo rectángulo, el lado más largo recibe el nombre de hipotenusa y los otros dos lados se llaman catetos.
3. Teorema de Pitágoras
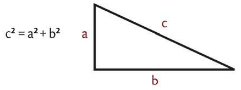
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Si un triángulo rectángulo tiene catetos de longitudes a, y b y la medida de la hipotenusa es c, se establece que:
4. Razones trigonométricas
Las razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado al ángulo entre ellos. Existen tres funciones trigonométricas fundamentales: seno, coseno, tangente. Y tres recíprocas: cotangente, secante y cosecante.
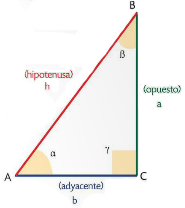
El seno de un ángulo, en un triángulo rectángulo, es igual a la razón entre las medidas del cateto opuesto a dicho ángulo y la hipotenusa.
Sen α = opuesto/ hipotenusa
El coseno de un ángulo, en un triángulo rectángulo, es igual a la razón entre las medidas del cateto adyacente al ángulo y la hipotenusa.
Cos α = adyacente/hipotenusa
La tangente de un ángulo, en un triángulo rectángulo, es igual a la razón entre las medidas del cateto opuesto y el cateto adyacente.
Tg α = opuesto/adyacente
La cotangente de un ángulo es la razón entre la longitud del cateto adyacente y su lado opuesto.
Cotg α = adyacente/opuesto
La secante de un ángulo es la razón entre la longitud de la hipotenusa y la longitud del cateto adyacente.
Sec α = hipotenusa/adyacente
La cosecante de un ángulo es la razón entre la longitud de la hipotenusa y la longitud del cateto opuesto.
Cosec α = hipotenusa/opuesto
Para hallar cada una de estas razones debemos conocer la magnitud de los lados del triángulo.
5. Relación entre sus ángulos
De acuerdo al gráfico del punto 4, sabemos que:
α + β + γ =180°. Debido a que la suma de los ángulos de un triángulo es igual a 180°.
El ángulo recto mide 90° y es el γ.
La suma de los otros dos ángulos también es 90°.
α + β = 90°
6. Relaciones entre lados y ángulos: razones trigonométricas
Razones de α:
sen α = a/h
cos α = b/h
tan α = a/b
7. Apliquemos lo aprendido con un ejemplo.
La hipotenusa de un triángulo rectángulo mide h=25 m y el cateto b = 20 m. Averiguar el valor de los ángulos β e γ, y la longitud del lado c. Ver datos en triángulo.
- Escribimos las razones del ángulo γ y vemos de cuál de ellas podemos obtener resultados.
cos γ = b/h
cos γ = 20/25 = 4/5
arc cos 4/5 = 36,38 ° γ = 36,86°
sen γ = c/h
sen 36,86° = c/25 c = sen 36,86° x 25 c=15m
- Calculamos el ángulo β.
β = 90°- γ = 90°-36,86°= 53,14°
