La recta numérica

---

La recta numérica es un gráfico unidimensional de una línea recta, fue introducida por John Wallis, un matemático Inglés que alrededor de 1670 la empleó para representar de modo gráfico los números naturales.

La recta numérica es propiamente una línea recta como lo indica su nombre que está marcada con intervalos regulares donde se colocan los números a representar. Originalmente solo se indicaban los naturales, pero más tarde se incluyeron los números negativos, que son los opuestos a los naturales (ℕ), y todos ellos forman los números enteros (ℤ).

Wallis solo representa los números naturales en la recta numérica,
es decir, desde el cero ‘0’ hasta el infinito ‘∞’.

Los números se colocan de tal manera que a medida que nos movemos hacia la derecha, sobre la recta, vamos encontrando números más grandes. Como se puede apreciar en la imagen, no existe un cero negativo, sino que este número es único.

Se representa en la figura desde el -8; al +8;, pero se entiende que la recta abarca desde -∞ a +∞.

El intervalo entre números consecutivos es el mismo, así que, si nos colocamos en el número +38, nos hemos desplazado 38 intervalos o posiciones a la derecha del cero. Y sí nos posicionamos en -52, nos hemos trasladado 52 intervalos a la izquierda del cero.

Con los números enteros es sencillo llevar un orden y una numeración sobre la recta numérica. No obstante, existen otros números que también se representan sobre la recta numérica pero que se ubican entre los intervalos de los números enteros. A este conjunto de números se los conoce con los nombres racionales, fracciones o quebrados. Se representan con la letra ℚ y se incluyen dentro de este grupo a aquellos números decimales que se pueden expresar como fracciones.

Aquellos números decimales que no pueden ser expresados como fracciones son denominados irracionales. Ejemplos de ellos son: 3,14159265… (π) y 2,728182845… (e). Este conjunto se expresa con la letra .

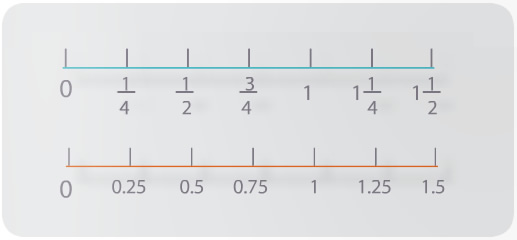
Se ven representadas algunas fracciones sobre un tramo de la recta numérica, y debajo los correspondientes números decimales.

La unión de los conjuntos de números ℤ, ℚ y dan origen al conjunto de números reales que se representa con la letra . No se ha incluido los ℕ ya que son parte de los enteros ℤ.

Si tomamos solo un intervalo de la recta numérica entre dos enteros, por ejemplo 3 y 4; se tienen infinitos reales entre esos dos números. Esto se deba a que el conjunto real es un conjunto no numerable, es decir, no se le puede asignar una función de números naturales que brinde todos los números reales.

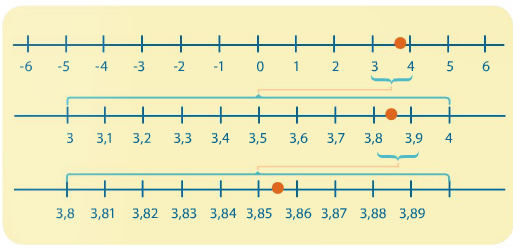
Haciendo un “zoom” en el intervalo (3,4) encontramos infinitos reales.

Generalmente, en las rectas numéricas no se representan todos los números reales porque quedarían repletas de números e indicaciones y se volvería dificultoso buscar y leer cierto punto. Es por ello que se emplea la siguiente representación tradicional.

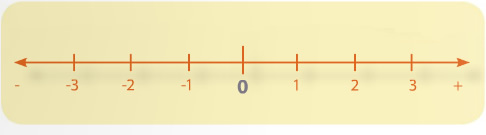
Se traza la recta numérica y se marcan los números enteros indicando con una punta de flecha a ambos lados de la recta denotando que se extiende a desde -∞ a +∞.

Representación de números irracionales

Para representar números irracionales como 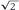, se puede emplear el teorema de Pitágoras.

Se traza la recta y se ubica el punto cero; a cada punto de la recta se le asocia un número real. Sobre la recta numérica se traza un cuadrado de lado uno, y una diagonal del mismo, partiendo desde el punto cero al vértice opuesto.

Al trazar una diagonal, el cuadrado queda dividido en dos triángulos rectángulos isósceles (2 lados iguales); en el cual se conoce el valor de sus lados y se desconoce el valor de la hipotenusa.

En el triángulo se puede hallar el valor de la hipotenusa c, mediante el teorema de Pitágoras. Se recuerda que el teorema relaciona los lados (catetos) con la hipotenusa.



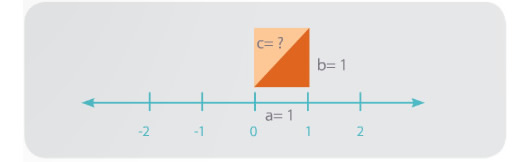
Entonces:

c²= a² + b²

Con los valores dados a= 1 y b= 1 se obtiene:

C²= 1² + 1² → C²= 1 + 1

C²=2 → c=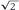

Luego, con un compás se hace centro en el punto de referencia cero y se traza un arco de circunferencia con una abertura igual a la longitud de la diagonal del cuadrado. Se llega así hasta un punto de la recta numérica y se marca el .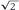



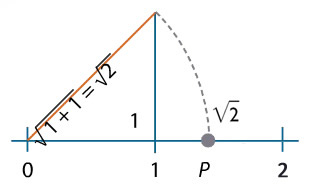
Esquema de cómo encontrar la ubicación en la recta numérica de un numero irracional con regla y compás.