 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
Las expresiones decimales no periódicas, con un número infinito de cifras después de la coma, representan los llamados números irracionales. Se le atribuye a Hipaso de Metaponto, un matemático y filósofo presocrático, el descubrimiento de estos números.

En el siglo V a. C. los pitagóricos (discípulos de Pitágoras) consideraban que los números racionales eran capaces de describir la geometría del universo. Hipaso comprobó la existencia de los números irracionales al intentar hallar la diagonal de un cuadrado que tiene a la unidad como lado y escribir la respuesta como un número decimal finito o una fracción. No pudo lograrlo, ya que dicha solución es √2 y ese número no tiene decimales finitos, dando origen al conjunto de números que hoy se denominan irracionales.
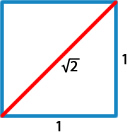
Hipaso era adepto a la escuela pitagórica, pero su descubrimiento contradecía la teoría de que los números racionales eran los que explicaban la geometría del universo. Esta postura ocasionó el rechazo de los pitagóricos y generó varias hipótesis acerca de su temprana muerte.
Versiones del fallecimiento de Hipaso de Metaponto:
LOS NÚMEROS IRRACIONALES MÁS CONOCIDOS
? : pi
Representa la relación entre la longitud de una circunferencia y su diámetro, en la geometría de Euclides. Es un número utilizado en varias áreas como matemática, física e ingeniería.
? = 3,1415926535897932384626433832795..
En el año 2010, Alexander Yee y Shigeru Kondo pudieron calcular 5.000.000.000.000 cifras de ? con una computadora Intel Xeon X5680 3.33GHz; 96GB RAM, la misma fue armada por Kondo. Mientras que Alexander Yee se encargó del software.
e : número de Euler
También denominado constante de Napier, fue utilizado para introducir el concepto de logaritmo por John Napier. Euler fue quien utilizó la letra e para representar dicha constante, en el año 1727. Es utilizado en cálculo, álgebra y números complejos.
e =2,7182818284590452353602874713527.
El logaritmo en base e, se denomina logaritmo natural o neperiano, está representado por la tecla que contiene la sigla ln en la calculadora.

? : número áureo o número de oro
También denominado razón de oro, es representado por la letra griega phi (?). Es considerado como el número de la proporción divina, ya que la misma se encuentra no solo en figuras geométricas, sino también en la naturaleza.
? = 1.61803398874989484820...
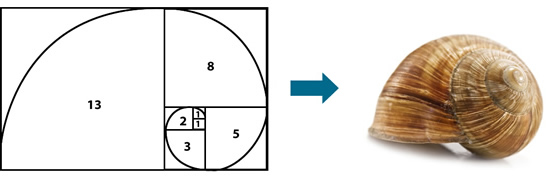
Espiral logarítmica, producto de la sucesión de rectángulos áureos.
Rectángulo áureo: Es el que cumple con la condición de que el cociente entre el valor del lado mayor y el lado menor da como resultado el número de oro.
Una antigua tradición habla de una "maravillosa copa de oro" construida por los griegos según directrices enunciadas en Egipto y Babilonia, de las que más tarde los cruzados tuvieron noticia en Bizancio y las difundieron en Occidente, donde fueron utilizadas por orfebres y arquitectos. Según estas directrices, la copa había de construirse de manera que su perfil reprodujera el esquematizado por la parte sombreada de la figura, que se obtiene trazando tres diagonales particulares de un pentágono regular. La proporción que guardan entre sí los dos segmentos en que una diagonal queda dividida por la otra, es un número irracional, que está relacionado con la llamada sección áurea de un segmento.
REPRESENTACIÓN EN LA RECTA NUMÉRICA
Existen métodos geométricos que permiten representar en la recta numérica algunos números irracionales.
Por ejemplo, si se desea representar √2 se puede realizar el siguiente procedimiento:
Se utiliza el Teorema de Pitágoras, utilizando un triángulo rectángulo isósceles, de catetos iguales a la unidad.
Teorema de Pitágoras: A2 = B2 + C2
B = 1
C = 1
Se reemplaza en la fórmula, el valor de B y de C.
A2 = 12 + 12
A2 = 1 + 1
A2 = 2
A = √2
De este modo se determina que la hipotenusa mide √2 y con un compás se la representa en la recta numérica, de la siguiente forma:

Se coloca la aguja de acero en el número cero y se abre el compás con una amplitud de √2. Luego se traslada esa medida a la recta numérica, obteniendo la ubicación de √2 en la misma.