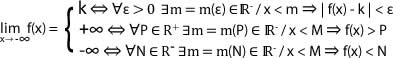Límite de una función en un punto

---

A veces, no podemos calcular directamente el valor de lo que buscamos, pero se puede conocer el resultado si nos acercamos cada vez más. El límite de la función f(x) en un punto x₀, corresponde al valor al cual las imágenes (y) se acercan cuando los originales (x) se acercan al valor x₀. Es decir, si llamamos "L" al límite, y "a" al valor al que se acerca x, podemos decir que:

"f(x) se acerca a L cuando x se acerca hacia a".

Tomaremos como ejemplo el límite de la función f(x) = x² en el punto x₀ = 2.

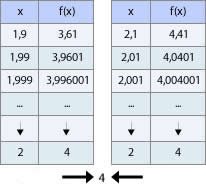
Tanto si nos acercamos a 2 por la izquierda o la derecha las imágenes se acercan a 4.

Se dice que la función f(x) tiene como límite el número L, cuando x tiende a x₀, si fijado un número real positivo ε, mayor que cero, existe un numero positivo δ dependiente de ε , tal que, para todos los valores de x distintos de x₀ que cumplen la condición |x - x0| < δ, se cumple que |f(x) - L| < ε.

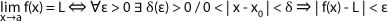
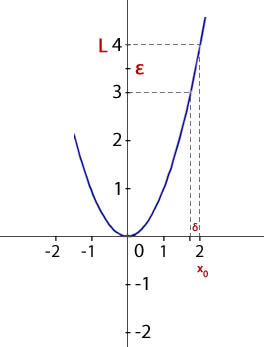
También es posible definir el concepto de límite a través de entornos:

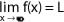si y solo si, para cualquier entorno de L que tomemos, por pequeño que sea su radio ∈, existe un entorno de x₀, E_δ(x₀) , cuyos elementos (sin contar x₀), tienen sus imágenes dentro del entorno de L, Eε(L).

Límites laterales

Diremos que el límite de una función f(x) cuando x tiende hacia a por la izquierda es L, si y solo si para todo ε > 0 existe δ > 0 tal que si x (a + δ, a) , entonces |f (x) - L| <ε.

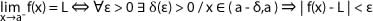
Diremos que el límite de una función f(x) cuando x tiende hacia a por la derecha es L , si y solo si para todo ε > 0 existe δ > 0 tal que si x (a, a + δ), entonces |f (x) - L| <ε.

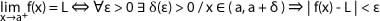
El límite de una función en un punto si existe, es único.

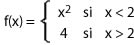
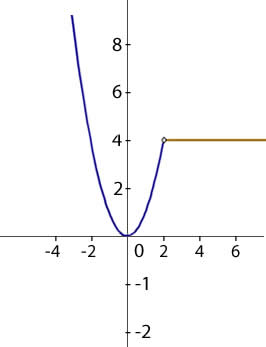
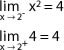
En este caso vemos que el límite tanto por la izquierda como por la derecha cuando x tiende a 2 es 4.

El límite de la función es 4 aunque la función no tenga imagen en x = 2.

Para calcular el límite de una función en un punto, no nos interesa lo que sucede en dicho punto sino a su alrededor.

Ejemplo

Dada la función:

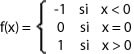
Hallar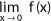   

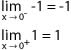
Como no coinciden los límites laterales, la función no tiene límite en x = 0.

Límites infinitos

Una función f(x) tiene por límite +∞ cuando x → a, si fijado un número real positivo K > 0 se verifica que f(x) > k para todos los valores próximos a a.

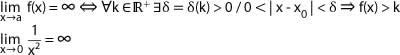
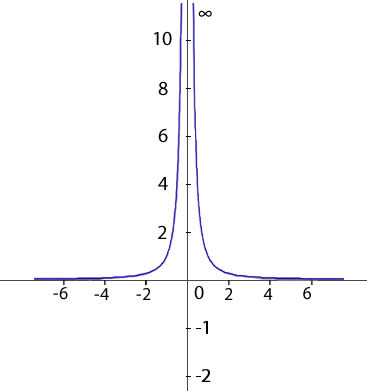
Límite menos infinito

Una función f(x) tiene por límite -? cuando x → a, si fijado un número real negativo K < 0 se verifica que f(x) < k para todos los valores próximos a a.

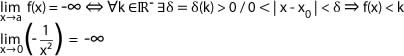
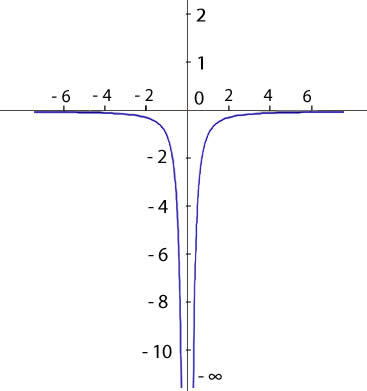
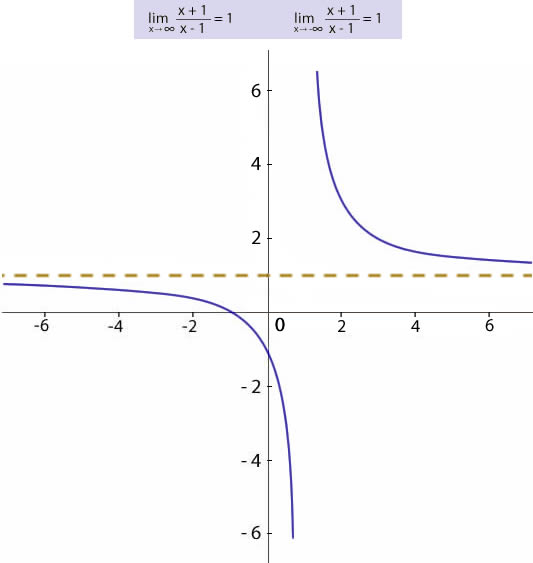
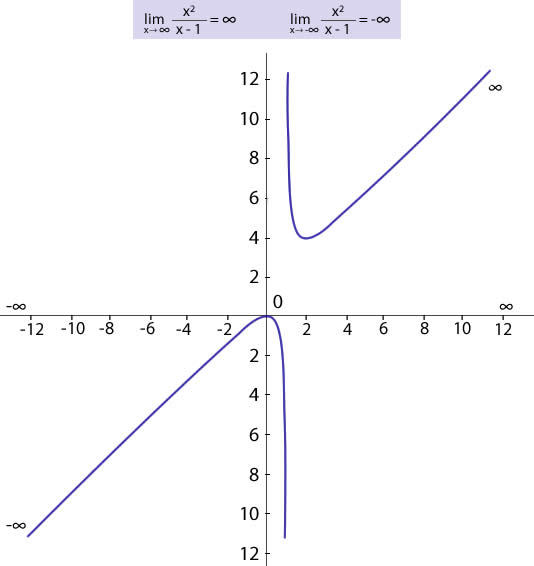
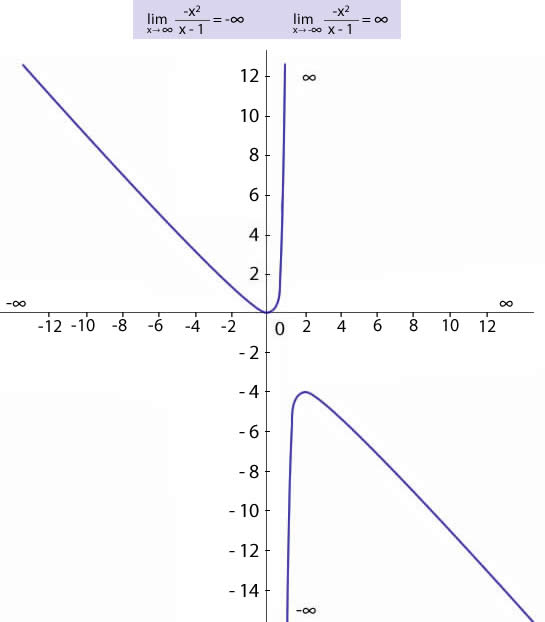
Límites en el infinito

Límite cuando x tiende a infinito

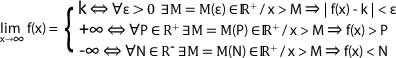
Límite cuando x tiende a menos infinito