 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
Cuando medimos una hoja de papel o la altura de una persona, estamos en presencia de medidas de longitud; al calcular a qué hora debemos salir de casa para llegar a tiempo a la escuela intervienen las unidades de tiempo; del mismo modo, las medidas de volumen y capacidad son muy útiles en la vida cotidiana.

El volumen de un recipiente determina su capacidad.
El volumen y la capacidad son dos conceptos que se relacionan entre sí pero que no tienen exactamente el mismo significado, veamos de qué se trata cada uno de ellos.
Volumen: Corresponde al espacio ocupado por un cuerpo. Su unidad de medida en el Sistema Internacional de Unidades es el m³.

El volumen de una caja está dado por el producto entre su largo, su ancho y su altura.
Capacidad: Es la propiedad que tiene un objeto de contener cierta cantidad de materia. Su unidad principal de medida es el litro (L).

Los envases que se utilizan para almacenar alimentos tienen distintas capacidades. Podemos llenarlos hasta completar su capacidad o no.
UNIDADES
Las unidades de volumen y capacidad pueden relacionarse entre sí mediante equivalencias.
UNIDADES DE VOLUMEN
El volumen se obtiene al multiplicar ancho por largo y por altura, dando como resultado una medida con unidad de longitud al cubo.
Veamos el siguiente ejemplo:

Calcular el volumen de una piscina rectangular de 40 m de largo, 25 m de ancho y 2 m de profundidad.
Datos:
largo: 40 m
ancho: 25 m
profundidad: 2 m
Sabemos que:
Volumen = ancho × largo × profundidad
Utilizando letras para identificar al ancho, al largo y a la profundidad, la fórmula queda expresada:
V = a × b × c
Reemplazamos los datos del problema en la fórmula:
V = 25 m × 40 m × 2 m = 2.000 m³
La unidad queda expresada al cubo porque la m fue multiplicada tres veces.
Por lo tanto, el volumen total de dicha piscina es de 2.000 m³.
En ocasiones es necesario hacer pasaje de unidades a otras mayores o menores. Para realizarlo es muy útil la siguiente tabla:
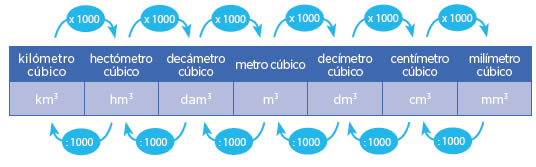
Cada vez que nos movemos una unidad a la derecha, multiplicamos por 1.000. Si nos movemos de derecha a izquierda, se debe dividir entre 1.000 por cada unidad.
Por ejemplo:
Si se desean convertir 5 m³ en cm³, ocurre lo siguiente:
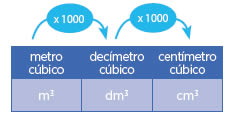
Nos movemos dos lugares a la derecha, por lo tanto:
5 × 1.000 × 1.000 = 5.000.000 cm³
UNIDADES DE CAPACIDAD
Del mismo modo que cuando trabajamos con volúmenes, a veces necesitamos hacer pasajes de unidades de capacidad. Para ello contamos con la siguiente tabla:
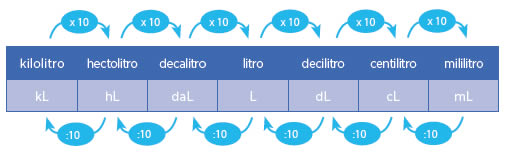
EQUIVALENCIAS ENTRE UNIDADES:
| 1 m3 = 1 kL | 1 dm3 = 1 L | 1 cm3 = 1 mL |
Vamos un problema de aplicación:
En una pecera cuyo volumen total es de 1.257 cm³ se coloca agua hasta ⅔ de su volumen. ¿Cuál es la capacidad de la misma? ¿Qué cantidad de agua se colocó?
Para calcular la capacidad, simplemente transformamos los 1257 cm³ de volumen en la medida de capacidad correspondiente:
1 cm³ = 1 mL
Entonces, 1.257 cm³ son 1.257 mL. Por lo tanto, la capacidad total de la pecera es de 1.257 mL.
Calculamos la cantidad de agua:
⅔ × 1.257 mL = 838 mL
De este modo podemos afirmar que la cantidad de agua que ocupa ⅔ del volumen total de la pecera corresponde a 838 mL.
Las aplicaciones que tienen el volumen y la capacidad son muy variadas, desde los envases que usamos cotidianamente, hasta los grandes túneles y construcciones que implican estrictos cálculos matemáticos.