Elementos en cuadriláteros

---

Los cuadriláteros, al igual que el resto de las figuras geométricas tienen lados, ángulos interiores, ángulos exteriores, vértices y diagonales. Aprendamos más acerca de ellos a continuación.

La palabra cuadrilátero significa "cuatro lados". Los segmentos denominados lados, pueden dibujarse de diversas formas: todos del mismo tamaño, de distintas medidas, con diferentes inclinaciones, etc. Pero lo fundamental es que esos cuatro segmentos estén unidos de forma tal que constituyan el contorno de una figura.

Sus cuatro lados son iguales de a pares, constituyen una figura geométrica: el rectángulo.

ELEMENTOS

Todos los cuadriláteros tienen:

• 4 lados.
• 4 ángulos interiores.
• 4 ángulos exteriores.
• 4 vértices.
• 2 diagonales.

lados: AB, BC, CD, DA.
angulos interiores: .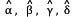
angulos exteriores: .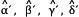
vertices: A, B, C, D.
diagonales: AC, BD.

La suma de los ángulos interiores de un cuadrilátero es 360º.
La suma de los ángulos exteriores de un cuadrilátero es igual a 360º.

CLASIFICACIÓN

Los dos grandes grupos en los que se pueden clasificar a los cuadriláteros son: paralelogramos y no paralelogramos.

PARALELOGRAMOS

La característica principal de los paralelogramos es que sus lados opuestos son paralelos.

PROPIEDADES

• Los lados opuestos son iguales.
• Tiene dos pares de lados paralelos.
• Los ángulos opuestos son iguales.
• Las diagonales se cortan entre sí, en segmentos iguales.
• El punto de intersección de las diagonales es el centro de simetría del paralelogramo.

Ejemplo:



• La base media de un paralelogramo es el segmento comprendido entre los puntos medios de los lados opuestos.

Ejemplo:

Las siguientes figuras son paralelogramos, por ello cumplen con las propiedades antedichas, pero además tienen propiedades particulares:

Cuadrado: tiene sus ángulos y lados iguales.
Las diagonales y las bases medias del cuadrado son ejes de simetría. Cada diagonal es bisectriz del ángulo recto.
Sus ángulos miden 900, es decir, son rectos. Por ello se lo denomina rectángulo.
Sus 4 lados son iguales, por lo que también es considerado un rombo.

Todo cuadrado es un rombo (cuatro lados iguales) y también un un rectángulo (tiene ángulos rectos).

Rectángulo: todos sus ángulos son iguales (rectos). Sus lados opuestos tienen la misma medida.
Las diagonales del rectángulo son iguales y son ejes de simetría. Las bases medias del rectángulo también son ejes de simetría de dicha figura.

Eje de simetría es el segmento que divide a la figura en dos partes iguales.

Paralelogramo: tiene dos pares de lados, aquellos que son opuestos, son paralelos e iguales.
Sus pares de ángulos consecutivos son suplementarios (suman 1800).
Sus diagonales no son perpendiculares entre sí.
Sus diagonales no miden lo mismo.

Rombo: tiene cuatro lados iguales. Sus ángulos opuestos miden lo mismo, son iguales dos a dos.

Las diagonales del rombo son: perpendiculares en su punto medio, bisectrices de los ángulos que atraviesan y ejes de simetría de dicha figura.

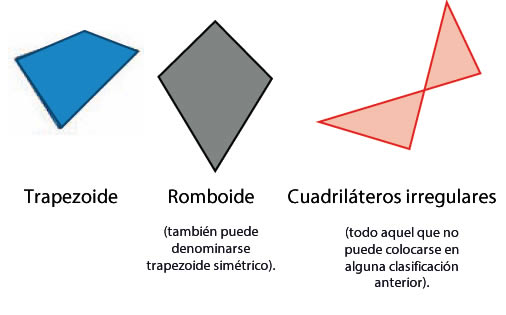
NO PARALELOGRAMOS

Pueden tener un único par de lados paralelos o ninguno.

Trapecios: Con un par de lados opuestos paralelos, denominados bases.
La altura del trapecio es un segmento perpendicular trazado desde un punto de una base a la otra.
El segmento que une los puntos medios de dos lados no paralelos se denomina mediana.

Trapecio isósceles: sus lados no paralelos son iguales.
Sus diagonales son iguales.

h: altura

Trapecio rectángulo: tiene dos ángulos rectos.

Trapecio escaleno: todos sus lados tienen distinta longitud.

La base media del trapecio es paralela a las bases e igual a la semisuma de ellas.

Sin pares de lados paralelos: