Números primos y compuestos

Los números naturales pueden clasificarse en primos y compuestos, dependiendo de la cantidad de divisores que tengan. A continuación aprenderemos todo sobre éstos y conoceremos algunos números muy particulares.

Para aprender matemática es necesario practicar un poco cada día.

Los números naturales son los enteros positivos: 1, 2, 3, 4,… Entre ellos se diferencian dos grandes grupos: primos y compuestos. Conocerlos es imprescindible para poder efectuar diversas operaciones con mayor rapidez y facilidad.

PRIMOS

Un primo es un número natural que a tiene dos divisores positivos: al uno y a sí mismo.

Ejemplo:

5 es primo, porque sus divisores son 1 y 5.

COMPUESTOS

Son aquellos que tienen más de dos divisores. Veamos algunos ejemplos:

15 es compuesto porque tiene cuatro divisores: 15, 5, 3, 1.

32 es un número compuesto porque tiene seis divisores: 32, 16, 8, 4, 2, 1.

COPRIMOS

Son los números primos entre sí. Esto quiere decir que ambos no tienen divisores comunes a excepción del 1. Por ejemplo: 6 y 11

Los divisores de 6 son: 6, 3, 2, .

Los divisores de 13 son: 13, .

Entre ellos solo tienen a 1 como divisor común.

Para comprender mejor qué son los coprimos, veamos un ejemplo de dos números que no cumplen con esta condición: 8 y 10

Los divisores de 8 son: 8, 4, , .

Los divisores de 10 son: 10, 5, , .

Los divisores que tienen en común el 8 y el 10 son dos, por lo tanto, no son primos entre sí.

DIVISIBILIDAD

Un número es divisible por otro cuando al efectuar la operación de división entre ellos, el resto es cero.

12 es divisible por
2 porque el resto
de la división
es 0.

13 no es divisible
por 2 porque el
resto de la división
no es cero.

Al conocer los números que componen a otro resulta sencillo descubrir cuáles son sus divisores:

21= 3 •7

Podemos decir que 3 y 7 son divisores de 21. Como además todo número (excepto el uno) es divisible por sí mismo y por 1, se desprende que:

21 es divisible por 21, 7, 3 y 1.

CRIBA DE ERATÓSTENES
La Criba de Eratóstenes es un procedimiento para identificar los números primos.

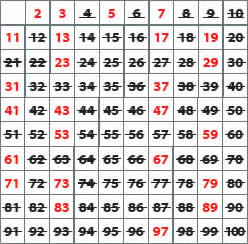Pasos para construir la Criba de Eratóstenes:

1º Comenzamos desde el número 2, que es el primer número primo, por lo tanto no lo vamos a tachar. Pero si eliminamos todos los siguientes múltiplos de 2: 4, 6, 8, 10, 12,…

2º El siguiente primo es el 3, así que debemos tachar todos los múltiplos de este número: 6, 9, 12, 15…

3º En esta instancia, ya tenemos gran parte de los números eliminados. Podemos observar que el siguiente número que aparece sin tachar es el 5, que sería el siguiente primo. Entonces, tachamos los múltiplos de 5 que aparecen a continuación: 5, 10, 15, 20…

4º Del mismo modo procedemos con el 7.

5º El siguiente número que aparece sin eliminar es el 11, pero… ¡Todos sus múltiplos están tachados! Por ello, aquellos números que han quedado sin descartar en esta instancia, son los primos.

Números especiales

Gemelos: Son números primos que entre ellos difieren en dos unidades. Ejemplos:
3 y 5, 5 y 7.

Repunit: En el sistema de numeración decimal un repunit es aquel cuyas cifras son repeticiones del número 1. Ejemplos:
11, 111, 1111.

Repidigit: Es similar al repunit, pero en este caso se conforma por la repetición de cualquier número natural. Ejemplos:
11, 33, 777, etc.

Capicúas: Son números que se leen igual de izquierda a derecha, que de derecha a izquierda. Ejemplos:
515, 61216, 222222, etc.

De Mersene: Un monje francés, Marin Mersene probó en 1644 que algunos números que cumplían con la expresión matemática 2n-1 eran primos. En la actualidad se conocen 48 números primos de Mersene. El primero de ellos surge al reemplazar a la n por 2, dando como resultado:
22 - 1 = 4 - 1 = 3
Por lo tanto 3 es el primer número primo de Mersene.