VOLVER A LOS ARTÍCULOS
Torta del cumpleaños de Matías, cortada en 12 porciones.
Repartir es una acción que se realiza en forma cotidiana. Las palabras “partes” y “porciones” son sinónimos, pero generalmente utilizamos porciones cuando nos referimos a alimentos, por ejemplo: cada niño comió dos porciones de pizza. Mientras que en lenguaje matemático el término utilizado es partes, que pueden ser representadas mediante fracciones.
Una fracción representa una división entre números, también se denomina expresión fraccionaria.
Estos números pueden tener las siguientes particularidades:
- El numerador es menor al denominador. En este caso se dice que la fracción es propia o pura.
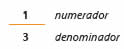
- El numerador es igual al denominador. La fracción es denominada aparente. Ej.: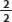 
- El numerador es mayor al denominador. A esta expresión fraccionaria se la denomina fracción impropia o impura. Ej.: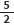 
Repartiendo
Cuando repartimos, estamos en presencia del primer caso. Dividimos a todo el objeto en partes iguales y obtenemos de este modo distintas fracciones. Veamos un ejemplo:
RESOLVER
Al cumpleaños de Matías asistieron 3 amigos: Jerónimo, Pablo y Verónica. Responder:
a) ¿Qué parte del total comió Pablo si se sirvió 2 porciones?
b) ¿Qué fracción representa la cantidad que comió Verónica? Ella aceptó una sola porción.
RESPUESTAS
a) El total siempre se escribe en el denominador de la fracción, es decir, debajo de la línea fraccionaria. La cantidad de partes que se han tomado del total se escribe arriba, en el numerador:
Por lo tanto, la fracción que representa a dos porciones de una tarta que está cortada en 12 partes es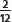
.
Recuerda siempre responder a la pregunta para que la resolución sea completa.
Rta.: Pablo comió 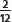del total.
b) Del mismo modo que en el ítem anterior, el numerador representa a la parte seleccionada del total y el denominador corresponde al total. En este caso, Verónica comió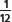 
de la tarta.
Rta.: La fracción que representa la cantidad que comió Verónica es .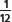
FRACCIONES
Como ya se ha mencionado, existen varios tipos de fracciones. Cuando deseamos comparar dos fracciones hay casos en los que esto se puede efectuar a simple vista, pero en otros se necesita un análisis matemático para lograrlo. Un método común es buscar fracciones equivalentes.
FRACCIONES EQUIVALENTES
Se obtienen al multiplicar al numerador y al denominador por un mismo número. A este procedimiento también se lo denomina amplificación.
Ejemplo: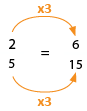
Del mismo modo, se pueden obtener fracciones equivalentes por simplificación. En dicho caso, se divide tanto al numerador como al denominador por el mismo número.
Ejemplo: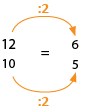
Comparación y orden de fracciones
Para poder ordenarlas, primero debemos lograr que todas tengan un mismo denominador y así poder identificar cuál es más grande y cuál más pequeña. La mejor manera de aprenderlo es con un ejemplo:
Ordenar en forma creciente las siguientes fracciones: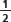 
, 
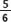y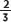 
.
Resolución:
Buscamos un denominador común a las tres fracciones, en este caso es el 6. El 6 es múltiplo de 2, 3 y 6, por ello se lo considera un “múltiplo común”.
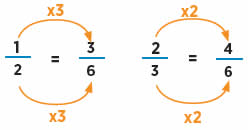
De este modo podemos comparar las fracciones porque tienen un denominador común. Nos queda: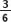
, 
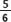y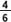 
.
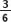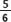
< Para dar la respuesta final, se deben colocar las expresiones fraccionarias dadas en el enunciado, éstas eran:
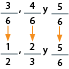
Así podemos ordenar, desde el numerador con menor valor hasta el mayor:
< <
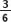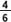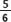
Por lo tanto, las fracciones del enunciado se ordenan del siguiente modo:
< <
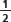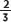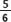
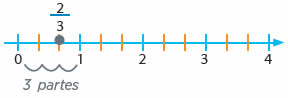
Representación en la recta numérica
Para representar una fracción en la recta numérica se divide a la unidad en tantas partes como indica el denominador. En el ejemplo siguiente se desea representar a la fracción 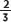, por ello se divide a la unidad en tres partes.
Luego se cuentan dos de las partes para ubicar la fracción, ya que el numerador indica la posición del número.
