VOLVER A LOS ARTÍCULOS
El valor de ϕ es 1,618033988…
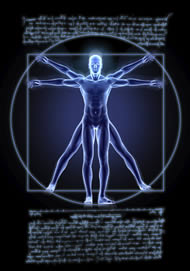
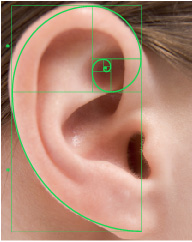La oreja humana tiene la forma de una espiral áurea.
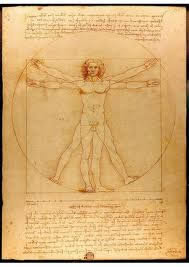Dibujo realizado por Leonardo da Vinci, realizando en tinta.
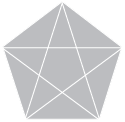La estrella pentagonal tiene proporciones áureas.
La proporción áurea que se esconde en la naturaleza y en muchas obras artísticas y arquitectónicas creadas por el hombre, es también denominada divina proporción. Ésta genera figuras de gran belleza y perfección.
El número de oro ϕ es un número irracional, es decir que no tiene fin. La proporción áurea en la naturaleza surge cuando al dividir dos longitudes de un mismo elemento, el resultado es igual o se aproxima al número áureo. Por ejemplo la longitud de la cabeza entre su ancho dan como resultado aproximadamente ϕ.
Fibonacci
Leonardo de Pisa, más conocido como Fibonacci, creó una sucesión infinita de números naturales que se denomina sucesión de Fibonacci.
La sucesión se crea partiendo de dos números 1:
1, 1,
Luego los siguientes términos son la suma de los dos anteriores:
1, 1, 2,
{
1+1 = 2
¿Por qué la denominación “divina” proporción?
En la obra De la Divina Proporción de Luca Pacioli surge esta forma de nombrar a la razón de oro. El fraile franciscano, relacionaba a las características de la proporción áurea con otras relacionadas a Dios. Entre ellas: Dios no puede ser definido, al igual que la proporción divina no puede ser expresada con una cantidad racional.
De ese modo se construye la sucesión, que al ser infinita se representa con tres puntos al final del último dígito que decidimos escribir.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,…
¿Es sencillo, cierto?
Lo más asombroso de esta sucesión es que cuando dividimos un número entre su anterior obtendremos aproximaciones al número ϕ. Al elegir números cada vez mayores, la aproximación se acerca más a dicho número.
Veamos dos ejemplos:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…
13 ÷ 8 = 1,625
233 ÷ 144= 1,61805…
233 ÷ 144 es más cercano a ϕ que 13 ÷ 8.
¿Intentas realizar el cálculo con los siguientes dos números consecutivos de la sucesión?
PATRONES EN LA NATURALEZA
Muchos vegetales y animales crecen siguiendo el patrón que determina una espiral logarítmica, generada por proporciones divinas. Entre los animales podemos dar como ejemplo a algunos caracoles que la presentan.
En algunos gasterópodos, se presenta la espiral logarítmica.
Número de oro y fractales en animales
Los equinodermos, además de presentar números de Fibonacci, muestran patrones fractales. Entre los equinodermos podemos nombrar a las estrellas de mar, los erizos de mar y ofiuras.
Las estrellas de mar poseen morfologías fractales y que responden a secuencias de Fibonacci.
En los vegetales abundan las relaciones entre la sucesión de Fibonacci y las formas que estos presentan. Si contamos los pétalos de algunas flores (lirios, margaritas, girasoles, etc.) podemos comprobar que poseen términos que corresponden a la sucesión anteriormente nombrada. También el crecimiento de algunas hojas se rige por números de Fibonacci.
En el Aloe espiralado, cuyo nombre científico es Aloe polyphylla, el crecimiento de sus hojas se realiza en forma de espiral de Fibonacci.
Ser Humano
En el ser humano existen diversas proporciones que dan como resultado la razón áurea. Algunas de estas relaciones son:
• La que existe entre la altura de los pies a la cadera y de los pies a la rodilla.
• La relación entre la altura de una persona y la altura hasta su ombligo.
• La que se presenta entre las falanges y la longitud de los dedos.
DIVINA PROPORCIÓN
Dados los segmentos:
A: segmento mayor
B: segmento menor
La divina proporción se determina por la siguiente ecuación:
A/B = (A + B)/A
“El cociente entre el segmento mayor y el menor es igual al cociente entre la suma de ambos segmentos entre el mayor de ellos.”
Las proporciones presentes en el ser humano se han estudiado desde la Antigüedad, siendo Leonardo da Vinci quien dejó dibujos y una amplia descripción de cada una de las regularidades presentes en el cuerpo del hombre.
El Hombre de Vitruvio
Da Vinci dibujó El Hombre de Vitruvio en el año 1490, tomando referencias de los trabajos del arquitecto Marco Vitruvio. Este dibujo, representa al hombre como centro del universo y las proporciones que debería poseer según los cánones clásicos de belleza. Las proporciones áureas abundan en dicho dibujo.
Las columnas del Partenón y las partes
del techo tienen proporción áurea.
SECCIÓN ÁUREA
Los griegos descubrieron la sección áurea, Platón hacía referencia a ella como “la sección”.
Sus estudios fueron la base de Euclides para realizar demostraciones sobre dicha razón.
Como es sabido, los griegos aspiraban a la belleza en todas sus formas, por ello diseñaban sus construcciones extremando los detalles para que tuviesen las proporciones adecuadas.
El Partenón de Atenas es un ejemplo de ello, donde la sección áurea está presente.
EL NÚMERO DE ORO Y LAS CONSTRUCCIONES
Las proporciones divinas se encuentran a nuestro alrededor, la forma de la escalera que se visualiza en la imagen esconde una espiral logarítmica.
Desde tiempos remotos el hombre ha tenido en cuenta las proporciones y cálculos matemáticos para crear estructuras que soporten distintos pesos y esfuerzos: puentes, viviendas, reservorios, transportes, etc. En sus inicios las construcciones se realizaban para solventar las necesidades del hombre, sin un requerimiento estético determinado.
Pero a lo largo de la historia, los arquetipos de belleza fueron cambiando y fusionándose en algunos casos.
La arquitectura utiliza a la matemática y la física como herramientas fundamentales para darle solidez a los diseños propuestos. En la actualidad, el diseño arquitectónico busca también como fin un de impacto visual e innovador.
EN EL UNIVERSO
En el Universo rige la Ley de Relatividad General de Albert Einstein, donde los Principios de Isaac Newton ya no dan todas las respuestas a los fenómenos que allí ocurren.
Einstein, a pesar de su genialidad, necesitó ayuda de matemáticos para que su teoría tuviese la rigurosidad que requería. Una anécdota muy conocida es la contestación del físico a una niña de 9 años:
“No te preocupes por tus problemas con las matemáticas; te aseguro que los míos son mucho mayores.”
Albert Einstein
Las galaxias se clasifican según su forma en: espirales, elípticas, lenticulares e irregulares.
Describir lo que ocurre en el espacio exterior es un poco más complejo, que lo relacionado al ámbito terrestre. Pero aun así podemos observar la geometría del resto del universo desde la Tierra, la forma de los planetas, las galaxias, la trayectoria de los cometas, etc. dejan ver a simple vista las perfectas proporciones.
PROPORCIONES EN EL ARTE
Los artistas utilizan proporciones asiduamente, ya sea una obra realista o abstracta, requiere de características como el equilibrio. Desde el arte rupestre ya pueden observarse registros de elementos matemáticos en éste, pueden verse espirales en petroglifos y cuevas, por ejemplo.
El arte del renacimiento en particular, es un ejemplo del uso de las proporciones divinas, La Mona Lisa de Da Vinci, Las Meninas de Velazquez, entre otras obras, pueden analizarse en función del rectángulo dorado.
En la actualidad las proporciones siguen vigentes, tanto en el arte como en otras ramas del conocimiento, porque el hombre siempre se ha interesado por la búsqueda de la belleza, el equilibrio y la armonía.
Espiral de Fibonacci
La representación geométrica de la sucesión de Fibonacci puede realizarse a través de la construcción de rectángulos áureos y estos permiten a su vez dibujar una espiral.
El rectángulo áureo es aquel cuya proporcionalidad entre los lados es igual al número de oro. A esta figura le podemos extraer un cuadrado que tenga como lados la medida del ancho del rectángulo y se obtiene otro rectángulo de oro. Este procedimiento se puede reiterar de forma indefinida. Todos los rectángulos convergen hacia un mismo punto, que es el vértice de una espiral, denominada espiral de Fibonacci.
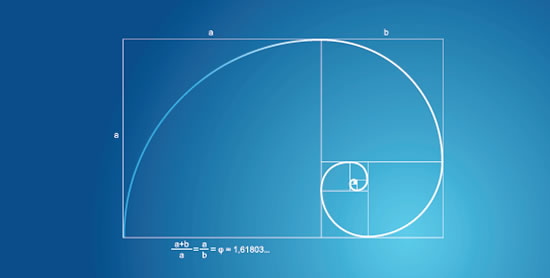
La espiral de Fibonacci es una aproximación a la logarítmica.
Estrella pentagonal
Estrella pentagonal Los pitagóricos utilizaban este símbolo para identificarse. Ellos denominaron números inconmensurables a los irracionales. Para los seguidores de Pitágoras, estos números contradecían su línea de pensamiento, ya que buscaban explicar al mundo por medio de números perfectos y los irracionales, según ellos, no lo eran. Sin embargo la estrella pentagonal que los representaba posee proporciones áureas.
