 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS

Los árboles tienen troncos y ramas, que a su vez se subdividen en otras. Por ello se denomina diagrama de árbol a una forma de organizar la información. En matemática es de gran utilidad para identificar en forma sencilla cómo agrupar distintos elementos.
Los diagramas de árbol se utilizan en matemática principalmente para identificar formas de agrupar elementos o para indicar los factores que conforman un determinado número.

Los diagramas de árbol se utilizan en matemática principalmente para identificar formas de agrupar elementos o para indicar los factores que conforman un determinado número.
Descomposición en factores
Al descomponer un número en sus factores primos podemos recurrir a dos procedimientos que nos facilitan el desarrollo. Uno de ellos es realizar divisiones sucesivas de un número entre números primos, hasta obtener cociente 1. Veamos el siguiente ejemplo:
Hallar los factores primos del número 36:
36
2
El primer número primo es el 2, por lo tanto dividimos al 36 entre 2.
36
18
2
El resultado de la división 36:2 es 18, este número se coloca debajo del 36.
36
18
2
2
El 18 es un número par, por lo tanto, podemos dividirlo entre 2.
36
18
9
3
1
2
2
3
3
El resultado de la división 18:2 es 9, el nueve no se puede dividir entre 2, pero si entre 3.
Dividimos 9:3 =3:
Y así sucesivamente hasta llegar a obtener un 1.
Del desarrollo anterior obtenemos:
36 = 2 • 2 • 3 • 3 Descomposición del número en factores primos.
36 = 22 • 32 Descomposición del número en potencias de factores primos.
Podemos obtener el mismo resultado por otro método: el diagrama de árbol. Vamos a hallar los factores primos del número 36 mediante dicho procedimiento.
Cuando utilizamos diagrama de árbol tenemos varias posibilidades de desarrollo, veamos dos de ellas para el caso del número 36:

¿Te animas a intentar otra forma de descomponer el número 36 mediante diagrama de árbol?
Agrupaciones
Al momento de agrupar cantidades pequeñas de elementos el diagrama de árbol permite visualizar todas las formas posibles de hacerlo. Para números grandes es conveniente utilizar las fórmulas de la combinatoria.
PROBLEMA:
¿De cuántas formas puede vestirse Lucas con las siguientes prendas?

Vemos que cualquiera sea el camino que decidimos tomar, el resultado es el mismo.
Utilizando los dibujos, podemos realizar el siguiente diagrama de árbol:
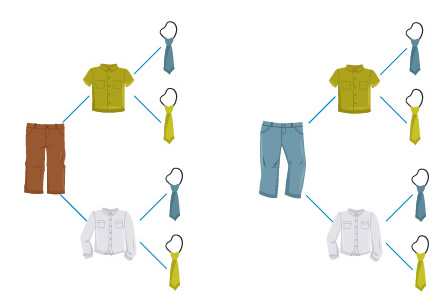
En total, Lucas tiene 8 posibilidades de seleccionar las prendas para vestirse.
En el problema anterior, vemos como se despliega el diagrama de árbol con imágenes, pero para agilizar la resolución de una forma matemática, representaremos con letras cada prenda:
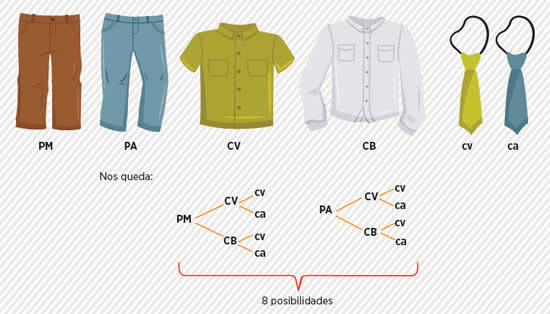
Probabilidad
Los diagramas de árbol también pueden aplicarse a experimentos probabilísticos de distinto tipo. Dentro de estos experimentos se encuentran los aleatorios, que son aquellos en los cuales no se puede predecir el resultado.
Espacio muestral: Conjunto de los resultados al realizar un determinado experimento aleatorio reiteradas veces.
Suceso: Cada uno de los resultados obtenidos al realizar el experimento aleatorio.
Regla de Laplace
Cuando todos los resultados son igualmente probables podemos aplicar la regla de Laplace. La misma determina que la probabilidad de que ocurra un suceso, cuando todos los sucesos elementales tienen la misma probabilidad de llevarse a cabo, se determina con la siguiente fórmula:

¿Cuál es la probabilidad de obtener un 2 al lanzar un dado?
Un dado tiene 6 caras, entonces los casos posibles serían 6. En una sola cara se encuentra representado el número 2, por lo tanto hay un solo caso favorable.
P (A) = 1/
6
Experimentos compuestos
Son aquellos que se conforman por varios experimentos simples. En el caso de experimentos compuestos, un procedimiento que suele utilizarse es el diagrama de árbol. Con éste se obtienen varias ramas que finalizan en sucesos simples, si se multiplican las probabilidades de estos sucesos se obtiene la probabilidad del suceso compuesto.
PROBLEMA:
¿Cuál es la probabilidad de obtener tres veces cara al lanzar una moneda tres veces seguidas?
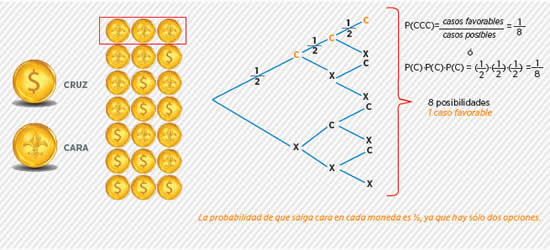
TOMA DE DECISIONES
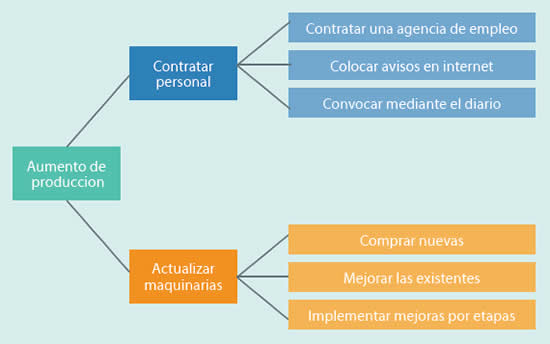
No solo en matemática suele utilizarse el diagrama de árbol como herramienta para resolver situaciones: en otras áreas, como en la gestión empresarial, suele emplearse para identificar las acciones necesarias para obtener un resultado deseado.
En este caso el “tronco” del árbol es la meta general y las “ramas” son las acciones a seguir, que se clasifican en niveles de importancia. Aplicando este método se puede desglosar una meta en objetivos y acciones que permitan su concreción.
ORGANIZACIÓN DE CONCEPTOS
Otro uso que se le da al diagrama de árbol es ordenar ideas de manera tal que puedan visualizarse las relaciones que se presentan entre ellas. Es una forma de organizar la información, partiendo desde una idea principal. De ésta surgen las “ramas” que corresponden a distintos niveles de jerarquía. Los diagramas de árbol, en este caso, se pueden utilizar como una técnica de estudio.

Para organizar la información al momento de estudiar son útiles los diagramas de árbol.
El diagrama de árbol tiene diversos usos y su importancia radica en el impacto visual que genera a simple vista. Permite comprender las relaciones entre el conjunto y el orden de jerarquía de los conceptos.