Movimiento y trabajo mecánico

Siempre escuchamos decir a muchos adultos: “Me voy al trabajo”. Del mismo modo los estudiantes suelen expresar en sus casas: “Estoy haciendo un trabajo en la computadora”. Sin embargo, en física existe otro uso diferente a esta cotidiana palabra y es este: el trabajo (W) es el producto de la fuerza aplicada (F) por la distancia (d), a lo largo de la misma dirección de la fuerza.

En física el trabajo es un principio de la mecánica, que comprende una fuerza y un desplazamiento; al trabajo (W) lo usamos para describir cuantitativamente lo que se obtiene cuando una fuerza hace mover a un cuerpo a lo largo de una distancia. El caso más sencillo es cuando se aplica una fuerza constante.

Trabajo debido a una fuerza constante

Para una fuerza constante F que actúa en la misma dirección del desplazamiento (Figura 1) el trabajo se define por la ecuación:

W = F • d (1)

Cuando tenemos una fuerza que mueve un cuerpo una distancia (d) y la fuerza aplicada posee un ángulo Ɵ respecto a la horizontal (Figura 2), la misma puede descomponerse en sus coordenadas Fx y Fy. Siendo Fx = F . cos Ɵ la componente de la fuerza paralela al desplazamiento, este análisis permite obtener una ecuación general:

W = F • d = F • cos Ɵ •d (2)

En donde la fuerza F es la suma de la componente paralela Fx más la componente perpendicular Fy, es decir F = Fx + Fy. A Fy la descartamos dado que no hace ningún efecto en la dirección del desplazamiento.

Es sencillo observar que cuando Ɵ =0° entonces la ecuación del trabajo (2) se transforma en la ecuación (1) por ser cos 0°=1.

El trabajo, a diferencia de la fuerza, es una magnitud escalar.

Figura 2: Trabajo realizado por una fuerza (F) constante que no tiene la misma dirección del desplazamiento.

La unidad del trabajo:

En el sistema internacional de unidades (SI) el trabajo se expresa en Joule (J). Un Joule es el trabajo necesario para trasladar un cuerpo una distancia de 1 m (metro) con una fuerza de 1 N (Newton).

1 J = 1 N . 1 m

FUERZA DE ROZAMIENTO Y TRABAJO

Cada vez que empujamos un objeto está presente la fuerza de fricción (Fr).

El niño empuja con cierta dificultad, debido a la fuerza de fricción presente entre el carrito y la superficie donde se desplaza, el suelo.

En una primera aproximación podemos decir que la fuerza de roce, rozamiento o fricción es constante, por lo tanto se puede apreciar en la imagen anterior que el trabajo realizado por dicha fuerza coincide en la dirección del movimiento pero se presenta en sentido opuesto. Por ello el trabajo de la fuerza de roce siempre será negativo:

W = - F_r • d = -μ • N • d

En donde μ es el coeficiente de fricción, N es el valor de la fuerza normal entre el objeto y la superficie y d, el desplazamiento o distancia recorrida.

¡Deduce! ¿Cuál de ellos es trabajo?

Te invitamos a deducir según los conceptos aprendidos, cuando se está realizando trabajo y cuando no, en los siguientes ejemplos:

1. Un niño aplica una fuerza sobre una pared y queda exhausto.

2. Una niña busca un libro en una biblioteca, mientras lo hace caen muchos libros al suelo.

3. En el Sistema Solar, un cometa es acelerado hacia el Sol.

4. Un hombre sostiene su maletín mientras espera el tren.

Respuestas:

1. La respuesta correcta es: ¡no!, este no es un ejemplo de trabajo. La pared no se desplazará y una fuerza debe ocasionar un desplazamiento para que ocurra trabajo.

2. La respuesta correcta es: ¡sí!, este es un ejemplo de trabajo. Hay una fuerza (de la gravedad) que actúa sobre los libros, causando un desplazamiento en la dirección de la caída.

3. La respuesta correcta es: ¡sí!, este es un ejemplo de trabajo. Hay una fuerza que hace que el cometa se desplace a través del espacio (podemos ver la cola del cometa, que muestra los gases expelidos mientras se traslada).

4. La respuesta correcta es: ¡no!, este no es un ejemplo de trabajo. Es cierto que el hombre está ejerciendo una fuerza contraria al peso del maletín, pero éste no sufre desplazamiento, está inmóvil.

El rol del ángulo en el trabajo

En la práctica, es decir en la vida cotidiana, podemos encontrar muchos ejemplos en donde la dirección de la fuerza aplicada no coincide con la del desplazamiento.

Analicemos la siguiente figura:

Recordemos que la fuerza total F será igual a las sumatoria de sus componentes F = Fx + Fy.

La ecuación del trabajo es:

W = F • d = F_x• d= F • cos Ɵ • d

en donde el cos Ɵ se obtiene a partir del teorema de Pitágoras.

a) Si la fuerza forma un ángulo de 90° con la dirección del desplazamiento, el trabajo es nulo.

b) Si el ángulo está comprendido entre 0° y 90°, el trabajo es positivo.

c) Si el ángulo está comprendido entre 90° y 180°, el trabajo es negativo.

Por lo tanto, el signo del trabajo dependerá de la dirección y sentido relativos a la fuerza ejercida y a su desplazamiento.

Potencia

Se llama potencia mecánica o simplemente potencia (P), a la variación del trabajo con respecto al tiempo.

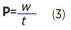
En otras palabras, es la rapidez con que se hace un trabajo. Este concepto es muy útil, ya que cierta cantidad de trabajo puede realizarse en diferentes intervalos de tiempo o velocidades, también mediante ella podemos distinguir no solo cuanto trabajo se realiza, sino también con cuanta rapidez se efectúa.

En la ecuación (3), las unidades resultantes son J/s:

Entre otras de las unidades comúnmente usadas tenemos el horsepower (hp) que equivale a:

1 hp = 746 W

Es importante resaltar que la potencia también indica cuanta energía se transfiere, por ejemplo en el motor de un auto cuyo medidor muestra los hp de potencia realizada.

Teorema del trabajo y la energía

Este teorema nos indica la relación que hay entre el trabajo y la energía. El concepto de energía es uno de los conceptos más destacados de las ciencias modernas, pues ésta es requerida por todos.

Paneles de energía solar cuya fuente es el Sol.

La energía está contenida en objetos y sistemas, recordemos que el trabajo se refiere a una fuerza sobre un objeto, mientras que la energía hace referencia a algo que los objetos tienen. Una forma de energía inseparablemente unida al trabajo es la energía cinética.

Un cuerpo que parte del reposo sobre una superficie sin fricción y al que se le ha aplicado una fuerza horizontal que actúa sobre él poniéndolo en movimiento puede ser representado por la siguiente imagen:

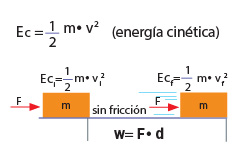
Diagrama del desplazamiento de un cuerpo en una superficie sin fricción.

¿A dónde fue el trabajo?

Debido a su movimiento decimos que el cuerpo tiene energía, que es llamada energía cinética.

Observando la figura anterior podemos calcular la diferencia del trabajo entre la posición inicial y la posición final, de la siguiente manera:

w = 1/₂ m • v 2f - 1/₂ m • v 2i = Ec_f - Ec_i = ΔEc
w_neto = ΔE_c

La ecuación anterior es conocida como el teorema del trabajo-energía y relaciona el trabajo neto realizado sobre un cuerpo con el cambio en su energía cinética. En otras palabras, el trabajo neto realizado sobre el cuerpo por una fuerza externa es igual al cambio de la energía cinética.

En resumen, ¿el trabajo es…?

Para que exista trabajo, desde el punto de vista físico, es necesario que estén presentes ciertas condiciones:

• Que se ejerza una fuerza.
• Que la fuerza se realice a lo largo de la dirección del desplazamiento.
• Que el desplazamiento no sea perpendicular a la fuerza.