LA REGLA DE CRAMER

---

Para obtener las soluciones de un sistema de ecuaciones se pueden elegir distintos caminos. Los resultados se pueden obtener por el método de Cramer, también mediante igualación, sustitución, reducción o gráficamente.

Para comprender la regla de Cramer es necesario recordar qué es un determinante:

DETERMINANTE 2X2

El determinante de una matriz cuadrada de segundo orden (2 filas x 2 columnas) es igual al producto de los elementos de la diagonal principal menos el producto de los elementos de la diagonal secundaria.

DP = diagonal principal , DS= diagonal secundaria.

¿QUÉ ES LA REGLA DE CRAMER?

Es un método utilizado en el álgebra para solucionar sistemas de ecuaciones lineales, mediante el uso de determinantes.

Los pasos a seguir para resolver un sistema de ecuaciones según la regla de Cramer son los siguientes:

Ejemplo:
Sea el sistema de ecuaciones lineales formado por dos ecuaciones con dos incógnitas:

Encontrar el valor de x e y mediante la regla de Cramer.

El primer paso, consiste en hallar el determinante del sistema (Δs). La matriz está constituida por los coeficientes de las incógnitas y el valor del determinante debe ser distinto de cero, es decir Δs ≠ 0.

Luego se deben encontrar los determinantes de cada incógnita.

Para ello se sustituye la columna de las x en la matriz, por los términos independientes:

Se sustituye la columna de las y en la matriz por los términos independientes:

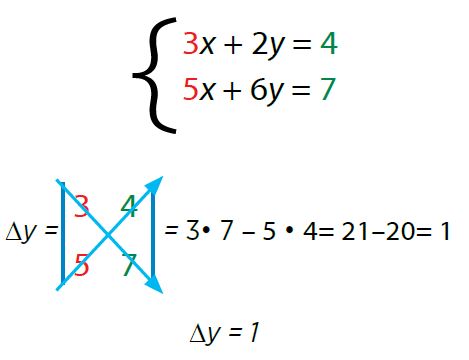
Por último para hallar el valor de las incógnitas, aplica la siguiente relación:

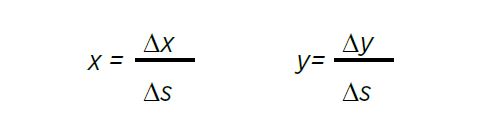
Sustituyendo:

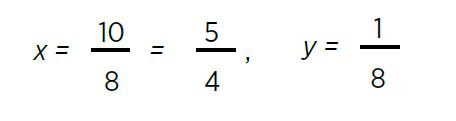
De acuerdo a lo anterior se puede enunciar la regla de Cramer así:

En matemáticas es importante prestar mucha atención y ante cualquier duda siempre es bueno consultar primero con tu profesor/a.

SISTEMAS DE ECUACIONES: OTROS MÉTODOS DE RESOLUCIÓN

Además del método de Cramer, puedes optar por:

Método de igualación

Este método consiste en despejar la misma incógnita en ambas ecuaciones y luego igualar las expresiones, resultando así una ecuación con una sola incógnita.

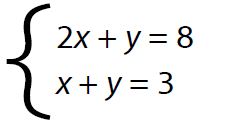
En primer lugar se despeja la misma incógnita en ambas ecuaciones.

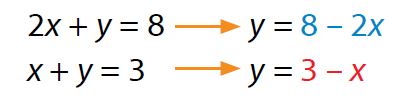
Se igualan las ecuaciones por medio de la variable común y:

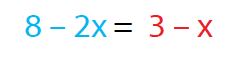
Se resuelve para obtener el valor de x:

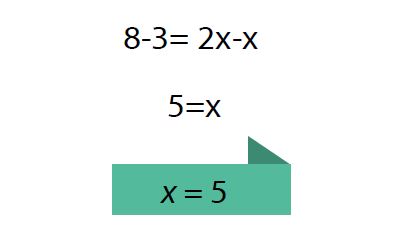
Una vez hallado el valor de x, se sustituye dicho valor en cualquiera de las ecuaciones principales para encontrar el valor de y.

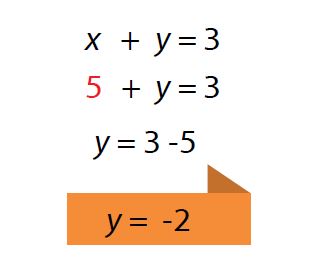
Al momento de resolver sistemas de ecuaciones, siempre es bueno recordar que hay varias formas de hacerlo.

Método de sustitución

Consiste en despejar una incógnita en una de las ecuaciones y sustituir en la otra. Esto con la intención de obtener una ecuación en función de una sola variable. El valor obtenido se sustituye en cualquiera de las ecuaciones principales y se resuelve, para así obtener el valor de la otra incógnita.

Ejemplo:

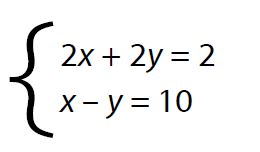
En primer lugar se despeja una de las incógnitas en una de las ecuaciones:

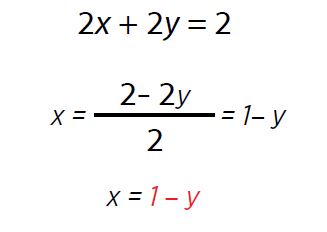
Se sustituye en la otra:

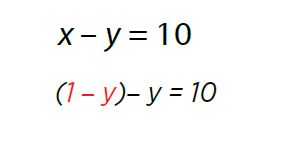
Se resuelve:

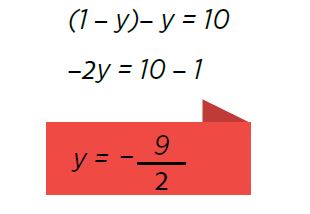
Por último se sustituye el valor de y en cualquiera de las ecuaciones principales para encontrar en valor de x.

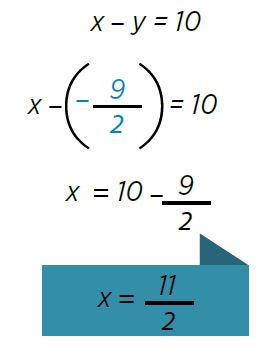
Método de reducción

En este método se preparan las dos ecuaciones para que una de las incógnitas tenga el mismo coeficiente en ambas pero con distinto signo. Al sumar las ecuaciones nos queda una ecuación con una sola incógnita. Que luego se resuelve del mismo modo que en los casos anteriores.

Ejemplo:

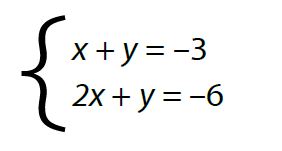
Se multiplica por -1 a la primera ecuación, en consecuencia, nos quedan los signos cambiados. Luego se suma algebraicamente.

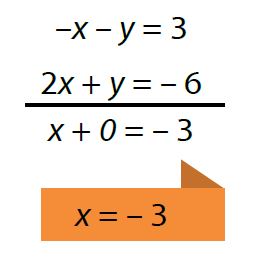
Donde el resultado x = – 3, se sustituye en cualquiera de las dos ecuaciones principales para así obtener el valor de y.

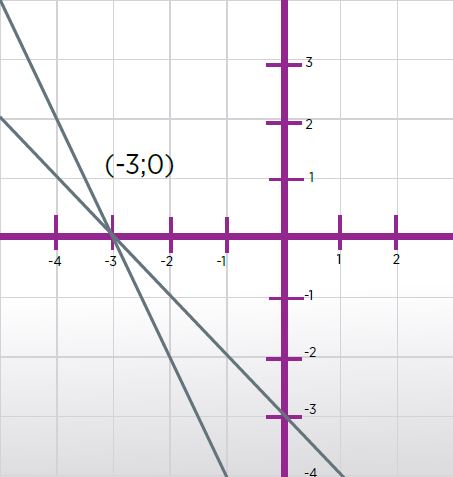
El método gráfico permite visualizar el punto de intersección de ambas rectas.

EL DESAFÍO DE LAS TRES INCÓGNITAS

Determinante 3x3

Dada una matriz A cuadrada de orden tres (3x3), se llama determinante de esta matriz al número real que se obtiene mediante el siguiente procedimiento:

A veces se dificulta el desarrollo de esta expresión tan complicada, por lo que surgen reglas nemotécnicas como la regla de Sarrus.

SISTEMA DE TRES ECUACIONES CON TRES INCÓGNITAS

Considérese el siguiente sistema de ecuaciones:

Primero encontramos el determinante del sistema (Δs) , dado que ahora se tienen tres ecuaciones con tres incógnitas, se debe utilizar el método de determinantes (3x3).

Quedando de la siguiente manera:

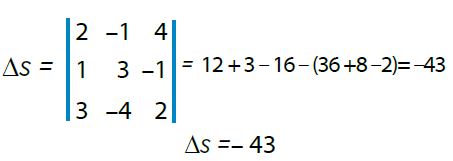
Ahora se deben hallar los determinantes de las incógnitas, tal como se hizo en el ejemplo anterior.

Por último, para hallar el valor de las incógnitas, se aplica la siguiente relación:

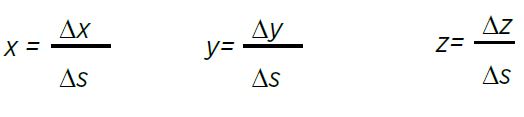
Sustituyendo,

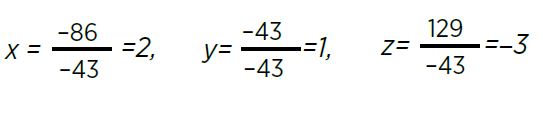
Existen otros métodos para resolver sistemas de ecuaciones como son: el método de Gauss, el método de la matriz inversa, el método gráfico, el método de eliminación de Gauss-Jordán, la descomposición de Cholesky, y muchos más.