Propiedades de raíces

---

En matemática la radicación es otra forma de expresar a la potenciación y al igual que esta última presenta ciertas propiedades importantes que se deben conocer al momento de resolver problemas de este tipo.

Raíz

Consiste en la obtención de un número que se ha multiplicado por sí mismo n veces bajo el operador de la raíz. Por eso también se conoce como “raíz enésima de un número”.

ⁿ√a = m

Sus elementos son:

• Radical (√): es el signo que representa la operación de la radicación.
• Índice de la raíz (n): indica las veces que ha sido multiplicado por sí mismo el resultado de la radicación. El índice de una raíz pertenece al conjunto de los números naturales y es diferente de cero.
• Radicando o subradical (a): es el producto de la multiplicación del resultado de la radicación según indique el índice de la raíz. El radicando pertenece al conjunto de los números reales.
• Raíz: es el resultado de la radicación propiamente, es el número que multiplicado por sí mismo tantas veces como indica el índice de la raíz da como resultado al radicando.

En el caso de la raíz cuadrada solamente se denota por el símbolo “√”.

Soluciones de una raíz

La solución de una raíz depende principalmente del radicando y del índice de la raíz. En algunas ocasiones puede tener una o dos soluciones y en otros casos puede que no tenga solución.

Radicando	Índice	Soluciones	Ejemplo
a ≥ 0	n par	Dos soluciones ±n√a	√4 = ± 2 Se cumple porque: (+2)(+2) = 4 (-2)(-2) = 4
	n impar	Una solución positiva +n√a	3√125 = +5 Se cumple porque: (+5)(+5)(+5) = 125 Al aplicar la regla de los signos no existe ninguna otra combinación posible que dé como resultado un número positivo como el radicando.
a ≤ 0	n par	No tiene solución, no existe ∄	4√-2 = ∄ no existe una raíz real En el caso del problema y considerando la definición de raíz se tiene que no hay ningún número que multiplicado cuatro veces por sí mismo dé como resultado un número negativo. Por lo tanto, la raíz no existe.
	n impar	Una solución negativa n√-a	3√-64 = -4 Se cumple porque: (-4)(-4)(-4) = -64 Al aplicar la regla de los signos no existe ninguna otra combinación posible que dé como resultado un número negativo como el radicando.

Al momento de resolver problemas con radicales es importante conocer la regla de los signos.

Propiedades de las raíces

1. Raíz de radicando cero: “toda raíz cuyo radicando sea cero es igual a cero, siempre y cuando su índice sea diferente de dicho número”.

Por ejemplo:

2. Raíz de la unidad: “la raíz de la unidad es igual a uno”.

Por ejemplo:

3. Raíz de un producto: “la raíz de un producto es igual al producto de las raíces de los factores”.

Por ejemplo:

4. Raíz de un cociente: “La raíz de un cociente es igual al cociente de las raíces del dividendo y del divisor”.

Por ejemplo:

5. Raíz de una raíz: “la raíz de una raíz es igual otra raíz con el mismo radicando y cuyo índice es igual al producto de los índices”.

Por ejemplo:

6. Potencia de una raíz: “la potencia de una raíz es igual a la misma raíz con el radicando elevado a dicha potencia”.

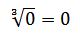
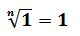
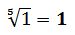
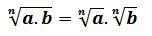
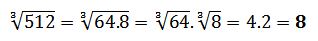
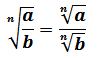
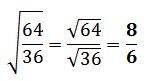
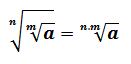
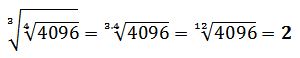
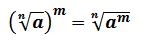
Por ejemplo:

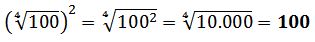
En la raíz aritmética de un número se cumple que (ⁿ√a)ⁿ = a.

Raíces y potencias de exponentes fraccionarios

Un radical puede expresarse en forma de exponente fraccionario en el cual el denominador de la fracción corresponde al índice de la raíz y el numerador al exponente del radicando.

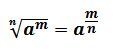
Por ejemplo:

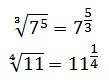
En el caso de radicales que se encuentren en el denominador, se pueden expresar también en exponentes negativos.

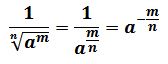
Por ejemplo:

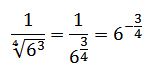
Como las raíces pueden expresarse en forma de exponente fraccionario, cumplen con las propiedades de las potencias.

Extraer factores fuera de un radical

En algunas ocasiones se busca expresar los radicales de formas más simples, para lo que se recurre a extraer factores en el radicando, en este caso, el exponente del factor que se va a extraer debe ser un múltiplo mayor o igual al índice de la raíz. Se cumple la siguiente expresión:

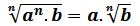El exponente del factor es igual al índice de la raíz.

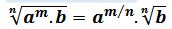El exponente del factor es múltiplo del índice y mayor que este.

Por ejemplo:

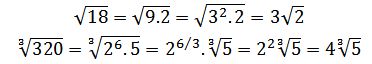
Cuando el exponente del factor es menor que el índice de la raíz no se puede extraer fuera del radical.

Suma de radicales

Los radicales pueden sumarse siempre y cuando sean semejantes, es decir, que tengan el mismo índice y radicando. En este caso se suman los coeficientes (los números que están fuera de la raíz) y se deja el mismo índice y radicando. Se cumple la siguiente expresión:

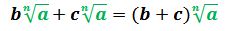
Por ejemplo:

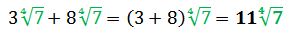
En algunos casos se pueden sumar radicales que no sean semejantes, para lograrlo se debe tratar de que los radicales sean semejantes por medio de la extracción de factores.

Por ejemplo:

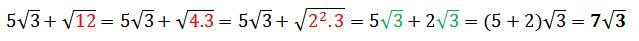
La descomposición de números en sus factores primos es muy útil para extraer factores de radicales.