Movimiento circular

La naturaleza está llena de ejemplos de diferentes tipos de movimientos. Tal es el caso del planeta Tierra, que ejerce un movimiento sobre su propio eje cada 24 horas; también el movimiento generado por un tocadiscos o un ventilador. Son ejemplos comunes de movimiento circular uniforme.

Ejemplos comunes de movimiento circular.
Conceptos básicos
- Eje: es el punto o línea fija en el centro de una circunferencia alrededor de la cual se realiza la rotación.
- Radio: es la distancia desde el centro de la circunferencia hasta cualquier punto de la misma.
- Posición: es el punto en el que se encuentra la partícula.
- Período: es el tiempo que tarda una partícula o un cuerpo en realizar una vuelta completa, revolución o ciclo completo. Se mide en segundos.
- Frecuencia: es el número de revoluciones, vueltas o ciclos que recorre una partícula en una unidad de tiempo. Se mide en hertz (Hz).
- Arco: es el espacio recorrido en la trayectoria circular o arco de radio unitario, partiendo de un centro fijo o eje de giro fijo, con el que se mide el desplazamiento angular. Su unidad es el radián.
Magnitudes
- Velocidad lineal o tangencial: es aquella que es tangente al punto o trayectoria en un instante y posee dirección y sentido de instante.
- Velocidad angular: es la variación del desplazamiento angular por unidad de tiempo.
- Aceleración lineal o tangencial: es la aceleración tangencial en el instante, es decir, es el producto de la aceleración angular y el radio del círculo.
- Aceleración angular: es la variación de la velocidad angular por unidad de tiempo.
- Aceleración centrípeta: es la aceleración que va dirigida hacia el centro de la trayectoria.
- Desplazamiento angular: es el desplazamiento efectuado en el movimiento circular y se obtiene mediante la posición angular en la que se encuentra en un momento determinado el móvil y al que se le asocia un ángulo determinado en radianes.
- Posición angular: es una magnitud que representa el ángulo que forma en cada momento el vector de posición de un cuerpo con el eje.
- Momento angular: es la magnitud que en el movimiento rectilíneo equivale al momento lineal o cantidad de movimiento pero aplicada al movimiento curvilíneo, circular y/o giratorio.
- Momento de inercia: es una cualidad que resulta de multiplicar una porción concreta de la masa por la distancia que la separa al eje de giro.
- Momento de Fuerza: es la fuerza aplicada por la distancia al eje de giro.

Ejemplo gráfico de aceleración lineal o tangencial.
Características del movimiento circular uniforme (M.C.U)
- La velocidad angular es constante (w = cte).
- El movimiento cuenta con aceleración normal, es decir, el vector velocidad es tangente en cada punto a la trayectoria y su sentido es el del movimiento.
- La rapidez es constante ya que tanto la aceleración angular como la aceleración tangencial son nulas.
- Existe un período (T), esto implica que las características del movimiento son las mismas cada T segundos.
- Existe una frecuencia (f), su valor es el inverso del periodo.

La velocidad como características del movimiento circular uniforme.
Fórmulas para movimiento circular uniforme (M.C.U)
| Período |
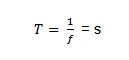 |
| Frecuencia |
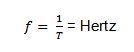 |
| Relación entre período y frecuencia |
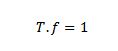 |
| Velocidad lineal o tangencial |
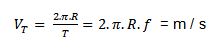 |
| Velocidad angular |
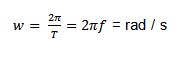 |
Relación entre velocidad tangencial
y velocidad angular |
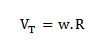 |
| Aceleración centrípeta |
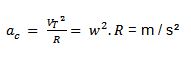 |
Donde:
R = radio
Fórmulas para movimiento circular uniformemente variado (M.C.U.V)
| Magnitud |
En términos lineales o tangenciales |
En términos angulares |
| Aceleración |
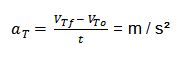 |
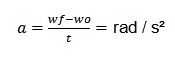 |
| Desplazamiento |
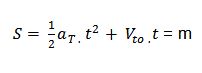 |
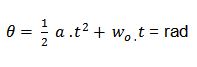 |
| Velocidad |
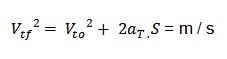 |
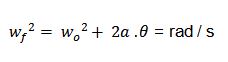 |
| Desplazamiento |
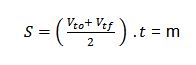 |
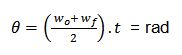 |
*Todo lo tangencial se obtiene al multiplicar lo angular por el radio.
Donde:
VTo = Velocidad tangencial inicial
VTf = Velocidad tangencial final
Wo = Velocidad angular inicial
Wf = Velocidad angular final
Problema 1 (M.C.U)
Una rueda de 0,5 m de radio gira a 180 revoluciones por minuto (r.p.m), calcular:
a) El módulo de la velocidad angular en rad/s.
b) El módulo de la velocidad lineal de su borde.
c) Su frecuencia.
Solución

Problema 2 (M.C.U.V)
Un CD-ROM de 0,06 m de radio gira a una velocidad de 83,33π rad / s. Si tarda en pararse 15 s, calcula:
a) El módulo de aceleración angular.
b) Las vueltas que da antes de detenerse.
c) El módulo de la velocidad angular para t= 10 s.
Solución

 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS



