 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
¿Sabías qué...?
Si los tres lados de un triángulo son números enteros entonces dichos números forman un trío denominado terna pitagórica.
Un teorema es una proposición matemática que se puede demostrar y uno de ellos es el de Pitágoras. Este teorema establece una relación entre los lados de un triángulo rectángulo y ha sido empleado en diversas áreas del conocimiento.
Los triángulos rectángulos
Son todos los triángulos conformados por un ángulo recto, es decir, un ángulo de 90 °. Un triángulo rectángulo está compuesto por una hipotenusa y dos catetos. La hipotenusa es el lado de mayor longitud de todos y se encuentra opuesta al ángulo recto. Los catetos son los lados menores y cada uno forma un ángulo agudo.

La suma de los dos ángulos agudos de un triángulo rectángulo siempre es igual a 90°.
Tipos de triángulos rectángulos
Dependiendo de la longitud de sus lados, este tipo de triángulo puede clasificarse en dos:
Triángulo rectángulo isósceles: es aquel triángulo rectángulo con sus dos catetos de igual longitud. En este tipo de triángulo cada ángulo agudo mide 45°.
Triángulo rectángulo escaleno: es todo triángulo rectángulo con catetos de diferente longitud.

La suma de los tres ángulos de un triángulo es igual a 180°.
El teorema de Pitágoras
Un filósofo griego descubrió que existía una relación los catetos y la hipotenusa de los triángulos rectángulos. Está proposición se llamó posteriormente “teorema de Pitágoras”.
Este teorema explica que el cuadrado de la hipotenusa en un triángulo rectángulo es igual la suma de los cuadrados de sus catetos. Suponiendo un triángulo rectángulo cuya hipotenusa mide a y la medida de los catetos es de b y c, se verifica que: a² = b² + c²

Conociendo dos lados de un triángulo rectángulo se puede calcular otro aplicando el teorema de Pitágoras.
Pitágoras de Samos
Nació en la Isla de Samos en el año 572 a. C. Fue un filósofo griego que impulsó la matemática y el pensamiento filosófico de la época. Se le atribuye la fundación de la Escuela pitagórica en la cual a pesar de que nunca dejó textos escritos, muchos de sus discípulos permitieron mantener su legado vigente.

Uno de los aportes más conocidos de Pitágoras fue el teorema que hoy lleva su nombre.
Demostración del teorema de Pitágoras
Existe una gran variedad de demostraciones que han realizado los matemáticos para validar el teorema de Pitágoras, cada una con una particularidad. Posiblemente, el mismo Pitágoras empleara una de estas demostraciones gráficas para verificar su postulado.
Una de las demostraciones más sencillas parte la configuración inicial de un triángulo rectángulo cuyos lados miden a, b y c, con sus respectivos cuadrados de sus catetos e hipotenusa (1).
Partiendo del triángulo rectángulo se construyen dos cuadrados diferentes:
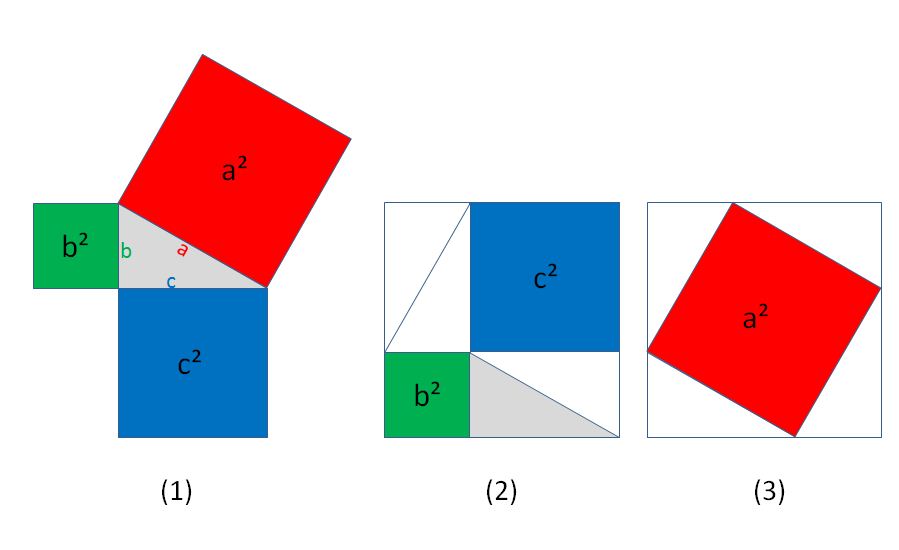
(2) El primero de ellos está constituido por los cuadrados de los catetos y cuatro triángulos rectángulos iguales al primer triángulo.
(3) El segundo cuadrado lo forman cuatro triángulos rectángulos iguales al inicial. La medida de los lados del cuadrado serán las misma que la longitud de los triángulos rectángulos, es decir, a.
Si en los cuadrados (2) y (3) se quitan los triángulos, se observa evidentemente que el área del cuadrado rojo es igual a a² y equivale a la suma de los cuadrados azul y verde (b² + c²), de esta forma se demuestra que a² = b² + c², quedando de esta forma verificado el teorema de Pitágoras.
Los egipcios y los triángulos
Antes de Pitágoras, los antiguos egipcios conocían que en un triángulo rectángulo de lados 3, 4 y 5 unidades de longitud se cumplía que al sumar el cuadrado de sus lados menores daban como resultado el cuadrado de la longitud de su hipotenusa
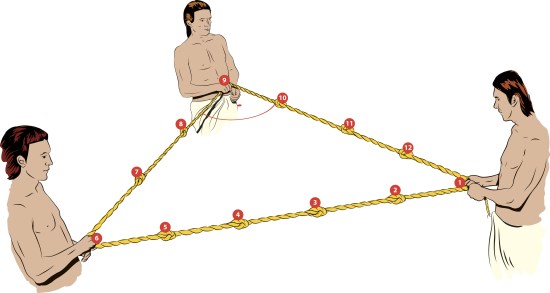
El triángulo sagrado egipcio era un triángulo rectángulo de 3, 4 y 5 unidades de longitud.
Practiquemos
Solución
Se aplica la fórmula:
b = √( a² - c² )
b = √( (10 cm)² - (8 cm)² )
b = √( 100 cm² - 64 cm² )
b = √( 36 cm² )
b = 6 cm
Recuerda que el cuadrado de la unidad de longitud se simplifica con la raíz.
Solución
Aplicamos la siguiente fórmula:
a = √( b² + c² )
a = √( (12 cm)² + (9 cm)² )
a = √( 144 cm² + 81 cm² )
a = √( 225 cm² )
a = 15 cm
Solución
Se aplica la siguiente fórmula:
c = √( a² - b² )
c = √( (35 cm)² - (21 cm)² )
c = √( 1225 cm² - 441 cm² )
c = √( 784 cm² )
c = 28 cm
Aplicaciones del teorema de Pitágoras
El teorema de Pitágoras es aplicado en otras áreas de la ciencia y en donde se requiere el análisis de una problemática, partiendo de triángulos rectángulos.
Solución
La diagonal del cuadrado divide a la figura en dos triángulos rectángulos iguales cuya longitud es igual a la hipotenusa de los mismos. Como se trata de un cuadrado, todos sus lados son iguales, es decir, los catetos de cada triángulo miden 3 m.
Aplicando el teorema de Pitágoras se tiene que:
d = √( (3 m)² + (3 cm)² )
d = √( 9 m² + 9 m² )
d = √( 18 m² )
d ≌ 4,242 m
Ejercicios propuestos
— Calcula el lado que falta en cada triángulo rectángulo
a)
b)
c)
Respuestas
Ejercicio de aplicación
- Determina la longitud de la escalera.
Respuesta: d ≌ 3,162