 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
Cuando se tiene una deuda en el banco se deben realizar una serie de abonos hasta saldar la deuda. Esta es solo una de las muchas situaciones en las que se emplean los numeros enteros y de allí la importancia de entender la regla de los signos en las diferentes operaciones matemáticas.
Adición y sustracción
En la adición de números enteros se pueden presentar dos casos diferentes:
- 5 + 4 = - 1
+ 5 - 4 = + 1
+ 5 + 4 = + 9
- 5 - 4 = - 9
PROBLEMAS COTIDIANOS
Una forma de entender la suma y resta de números enteros es relacionándolos con la vida cotidiana, donde los números positivos representan la cantidad de dinero que tengo, en tanto los números negativos representan la cantidad de dinero que debo, por ejemplo: Sofía debe 10 pesos y abona 5 pesos de su deuda, ¿cuánto le falta por pagar?
Datos:
Ana debe => Número negativo
- 10 pesos
Ana abona => Número positivo
+ 5 pesos
Calculo:
- 10 + 5 = - 5
Respuesta:
A Sofía le restan por pagar 5 pesos.
En la resta de números enteros se transforma la operación en una adición del opuesto, por ejemplo:

Multiplicación y división
En la multiplicación y división, la regla de los signos dice que aquellas operaciones que involucren números con signos iguales dan como resultado un número positivo, en tanto, las operaciones cuyos números posean signos diferentes dan como resultado un número negativo. Por ejemplo:

¡APLICANDO LO APRENDIDO!
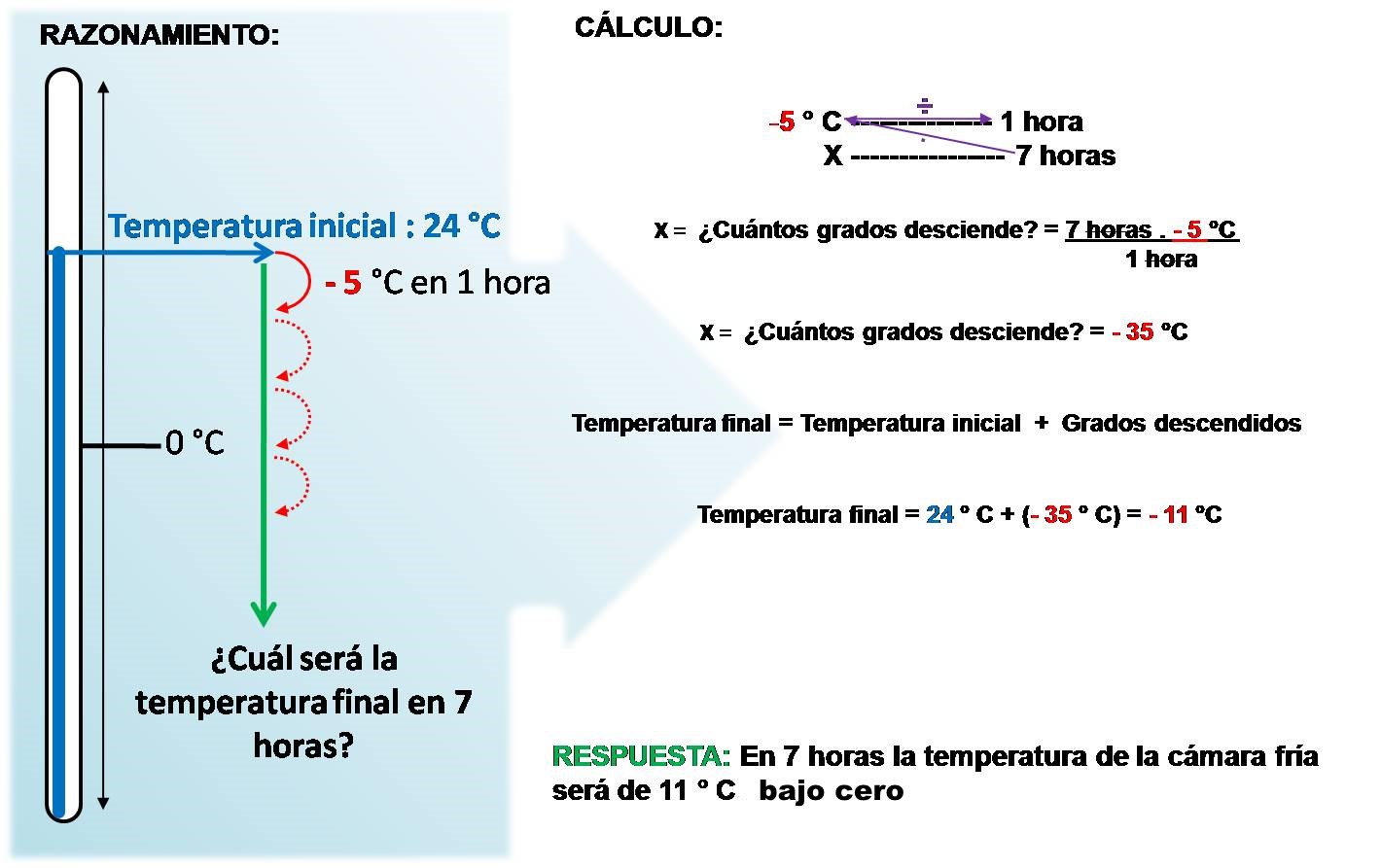
En una cámara de frío la temperatura desciende 5 °C por hora. Si la temperatura inicial es de 24 °C, ¿cuál será la temperatura luego de 7 horas?
|
Multiplicación |
División |
||||||||
|
+ |
. |
+ |
= |
+ |
+ |
÷ |
+ |
= |
+ |
|
- |
. |
- |
= |
+ |
- |
÷ |
- |
= |
+ |
|
+ |
. |
- |
= |
- |
+ |
÷ |
- |
= |
- |
|
- |
. |
+ |
= |
- |
- |
÷ |
+ |
= |
- |
Potencia
En el caso de las potencias se pueden presentar dos casos:
En las potencias de número positivos el resultado siempre es otro entero positivo.
(+a)n
Donde n puede ser par o impar.
Ejemplo:
(+ 2)2 = (+ 2) . (+ 2) = + 4
(+ 2)3 = (+ 2) . (+ 2) . (+ 2) = + 8
En las potencias de números negativos, el signo del resultado depende del exponente. Cuando el exponente es par el resultado es un número positivo, mientras que si el exponente es impar el resultado es un número negativo.
(-a)n
Donde n puede ser par o impar.
Ejemplo:
(- 3)2 = (- 3) . (- 3) = + 3
(- 3)3 = (- 3) . (- 3) . (- 3) = - 27
Ejercicios
1. Resuelve las siguientes sumas y restas de números enteros.
2. Resuelve las siguientes multiplicaciones y divisiones de enteros.
3. Resuelve las siguientes potencias.
4. Resuelve los siguientes problemas.
|
Equipo |
Partidos Ganados |
Partidos empatados |
Partidos Perdidos |
Goles a favor |
Goles en contra |
Puntaje |
|
Rojo |
5 |
3 |
2 |
25 |
15 |
18 |
|
Azul |
6 |
0 |
2 |
24 |
13 |
18 |
¿Qué equipo debe pasar la eliminatoria?
c) Ana tiene 50 $ y le debe 5 $ a cada uno de sus amigos. Si tiene 6 amigos, contesta:
- ¿Cuánto dinero debe en total? ¿Es un número negativo o positivo?
- ¿Cuánto dinero le queda? ¿Es un saldo positivo o negativo?
5. Completa con los signos correctos.