 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
De la matemática se deriva una rama que se encarga de estudiar todo lo referente a las figuras geométricas: la geometría. Esta rama también se encarga del estudio de propiedades como el área y el perímetro de las figuras geométricas. A continuación estudiaremos el área.
El área de las figuras geométricas se refiere al espacio o superficie comprendida dentro de un perímetro y puede calcularse utilizando la fórmula correspondiente a cada figura.
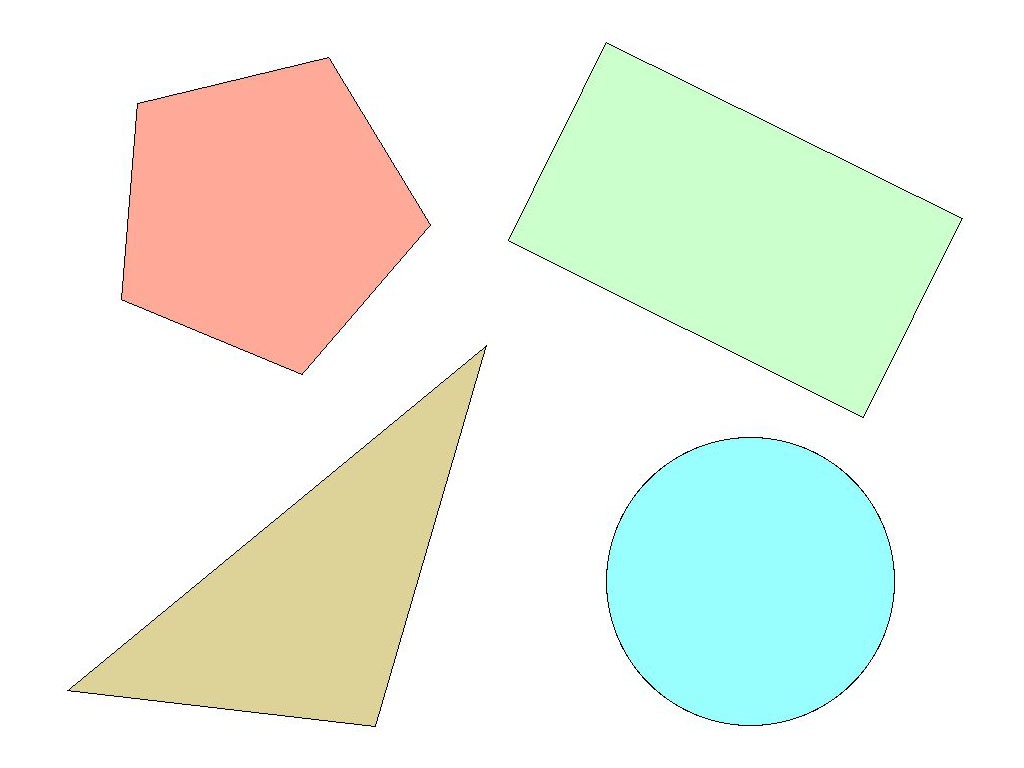
Figuras geométricas planas básicas.
Área de un triángulo
El triángulo es un polígono caracterizado por poseer tres lados que dan origen a tres vértices y a tres ángulos internos. Debido a sus características, es considerado la figura más simple después de la recta en la geometría.
Para calcular el área de un triángulo se utiliza la siguiente fórmula:
Donde:
b = base del triángulo
h = altura del triángulo
Ejemplo:
Hallar el área de un triángulo cuya base es 12 cm y su altura es 8 cm.
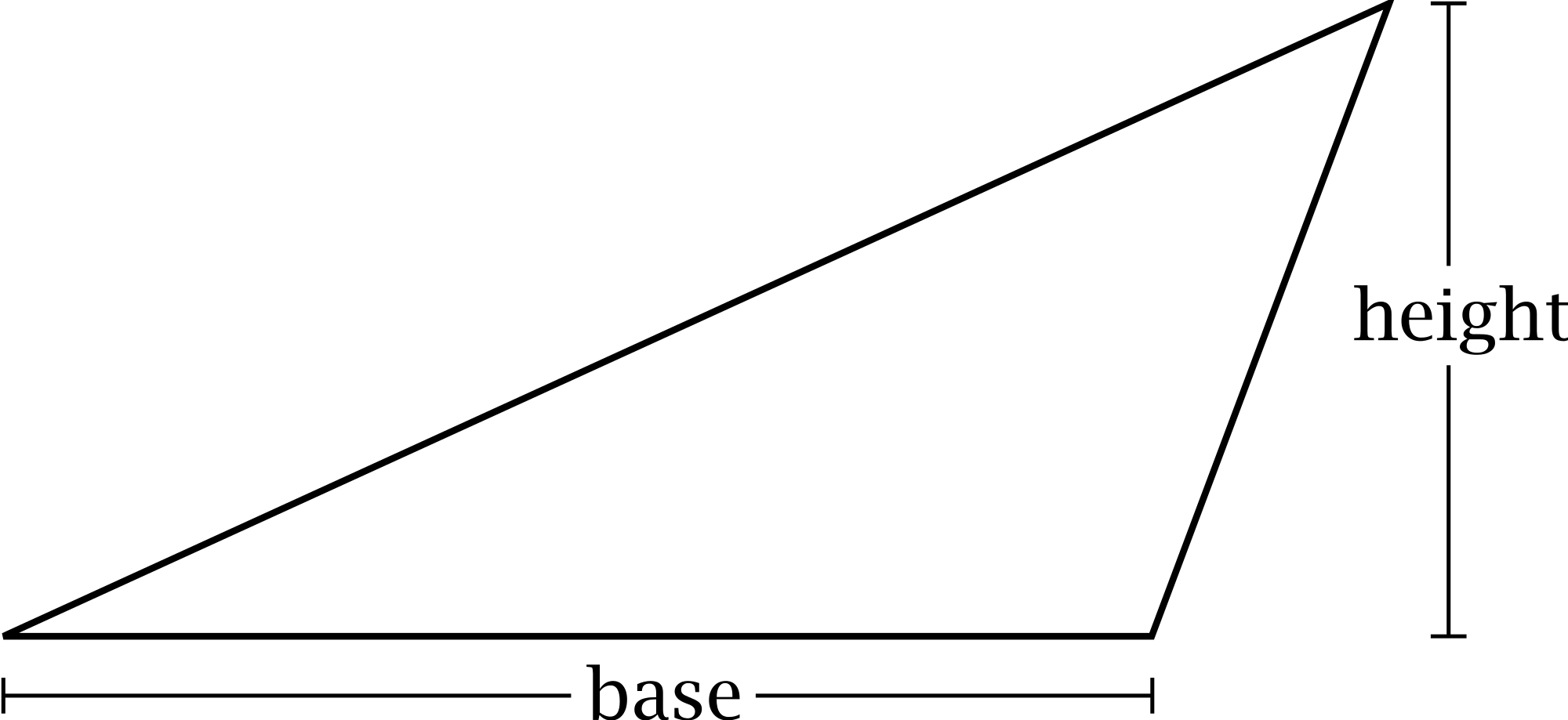
El triángulo y sus partes.
Área de un cuadrado
El cuadrado es un paralelogramo ya que está constituido por 4 lados que miden lo mismo y son paralelos dos a dos. Los 4 ángulos internos de un cuadrado son ángulos rectos.
Para calcular el área de un cuadrado de utiliza la siguiente fórmula:
Donde:
L = longitud de los lados del cuadrado
Ejemplo:
Hallar el área de un cuadrado de 8 cm de lado.
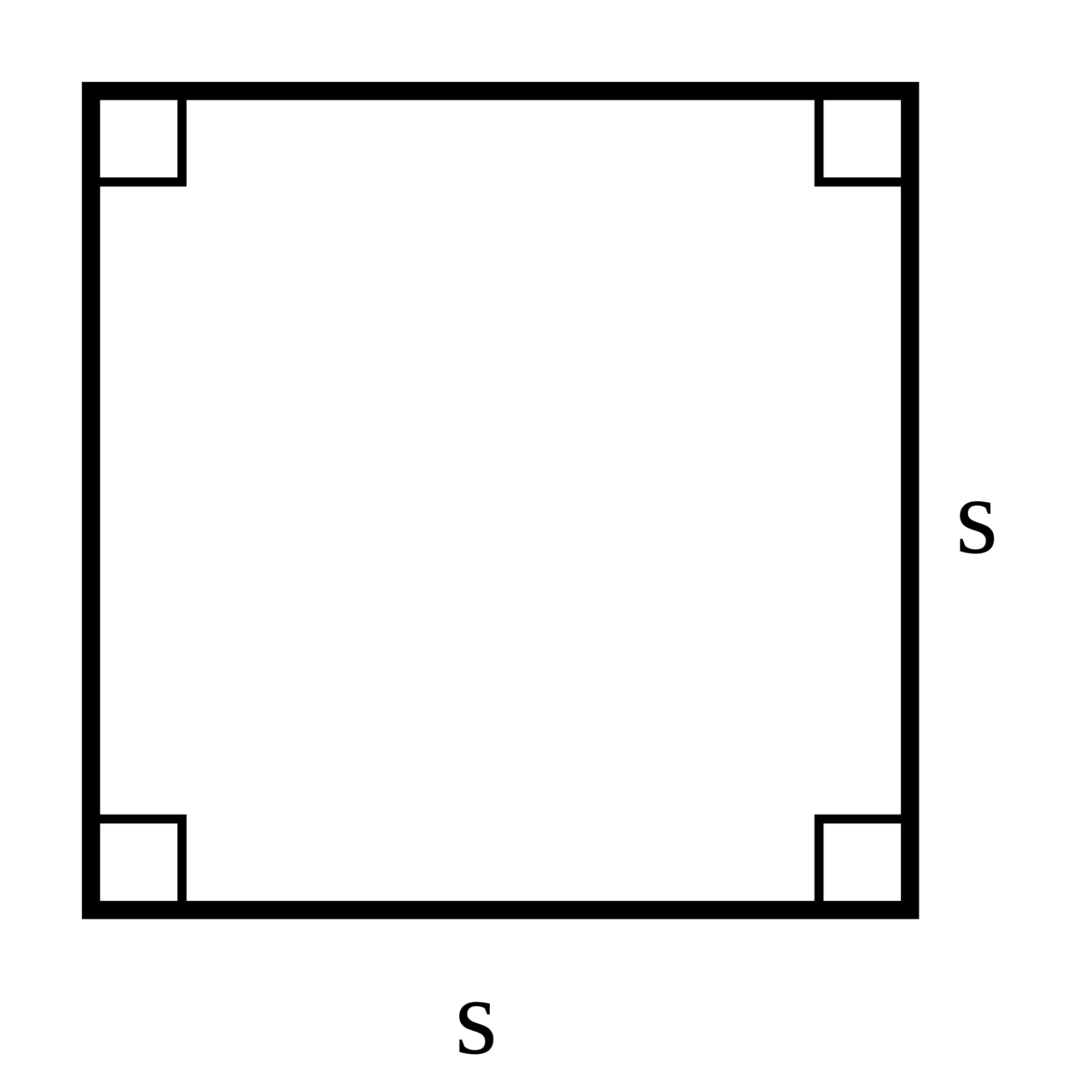
El cuadrado y sus lados.
Área de un rectángulo
El rectángulo es un paralelogramo ya que está constituido por 4 lados, cuyos lados opuestos tienen la misma longitud, y sus ángulos internos forman 4 ángulos rectos.
Para calcular el área de un rectángulo se utiliza la siguiente fórmula:
Donde:
b = base del rectángulo
h = altura del rectángulo
Ejemplo:
Hallar el área de un rectángulo cuya base es 6 cm y su altura 4 cm.
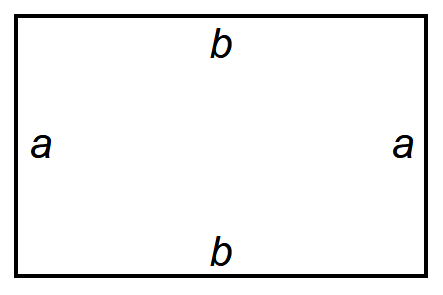
El rectángulo y sus lados, donde b es base y a es altura.
Área de un rombo
El rombo es un paralelogramo ya que está constituido por 4 lados iguales y 4 ángulos internos iguales dos a dos. Las diagonales del rombo se cortan perpendicularmente.
Para calcular el área de un rombo se utiliza la siguiente fórmula:
Donde:
D = diagonal vertical del rombo
d = diagonal horizontal del rombo
Ejemplo:
Hallar el área de un rombo cuya diagonal vertical mide 35 cm y la diagonal horizontal mide 18 cm.
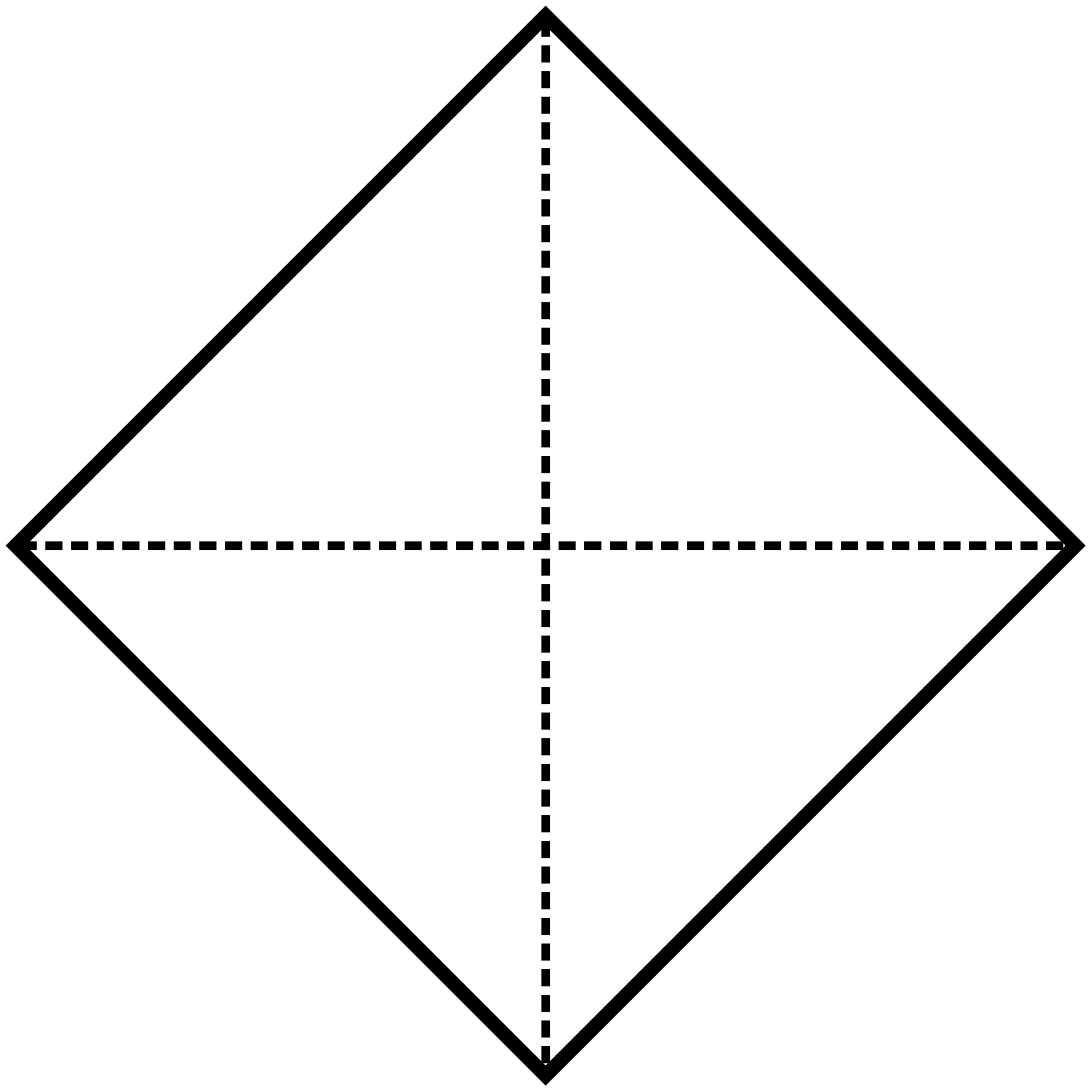
El rombo y sus diagonales perpendiculares.
Área de un romboide
El romboide es un paralelogramo que tiene dos ángulos y sus lados iguales dos a dos, característica que lo hace diferente del rombo y del rectángulo.
Para calcular el área de un romboide se utiliza la siguiente fórmula:
Donde:
b = base del romboide
h = altura del romboide
Ejemplo:
Hallar el área de un romboide cuya base es 10 cm y su altura 8 cm.
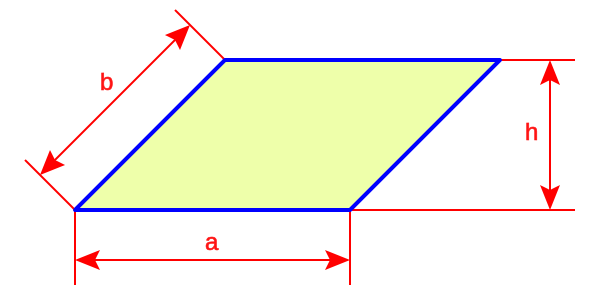
El romboide y sus partes.
Área de un trapecio
El trapecio es un polígono de 4 lados constituido por dos lados paralelos denominados base mayor y base menor. Los 4 ángulos internos que lo conforman son diferentes a 90°.
Para calcular el área de un trapecio se utiliza la siguiente fórmula:
Donde:
B = base mayor del trapecio
b = base menor del trapecio
h = altura del trapecio
Ejemplo:
Hallar el área de un trapecio cuya base mayor es 15 cm, su base menor es 8 cm y su altura es 10 cm.
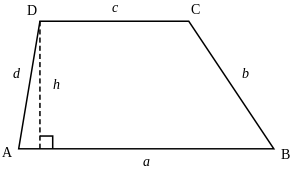
El trapecio y sus lados.
Área de un polígono regular
Un polígono regular es aquel que posee lados y ángulos interiores iguales.
Para calcular el área de un polígono regular se utiliza la siguiente fórmula:
Donde:
P = perímetro del polígono regular
a = apotema del polígono regular
Ejemplo:
Hallar el área de un polígono regular cuyo perímetro es 50 cm y su apotema es 5 cm.
El pentágono es un polígono regular.
Para practicar: