VOLVER A LOS ARTÍCULOS
La matemática está compuesta por numerosos tipos de operaciones que varían según su complejidad. Entre esas operaciones se encuentra la potenciación, que consiste en la multiplicación de factores iguales de acuerdo a un exponente y cuyos ejercicios se realizan siguiendo una serie de propiedades.
La potenciación también es definida como la forma abreviada de escribir un producto formado por varios factores iguales. Esta operación matemática está constituida por dos factores: la base o número que se debe multiplicar por sí mismo y el exponente o número superior que indica cuántas veces debe multiplicarse la base. Por ejemplo:
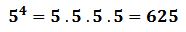
Donde:
5 = es la base de la potencia
4 = es el exponente de la potencia
Partes de una potencia.
A continuación se muestran las propiedades de la potencia y cómo deben aplicarse de forma correcta.
| Propiedades de la potencia | Representación | Ejemplos |
|---|---|---|
|
Potencia de exponente 0 |
|
|
|
Potencia de exponente 1 |
|
|
|
Potencia de exponente negativo |
|
|
|
Multiplicación de potencias de igual base |
|
|
|
División de potencias de igual base |
|
|
|
Potencia de una potencia |
|
|
|
Potencia de exponente racional |
|
|
|
Multiplicación de potencias con el mismo exponente |
|
|
|
División de potencias con el mismo exponente |
|
|
Ejercicio 1
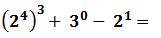
Se aplican las propiedades de la potencia necesarias:
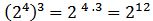→ potencia de una potencia
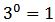→ potencia de exponente cero
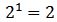→ potencia de exponente uno
Quedando la operación de la siguiente manera:
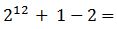
Se resuelven las potencias posibles:
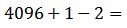
Se resuelven las sumas y restas:
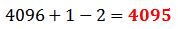
Ejercicio 2
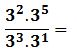
Se aplican las propiedades de la potencia necesarias:
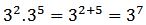→ multiplicación de potencias de igual base
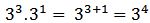→ multiplicación de potencias de igual base
La operación queda de la siguiente manera:
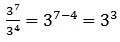→ división de potencias de igual base
Se resuelven las potencias posibles:
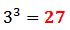
Ejercicio 3
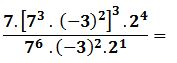
Se aplican las propiedades de la potencia necesarias:
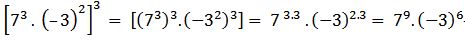→ potencia de una potencia
L operación queda de la siguiente manera:
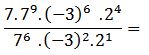
Luego:
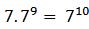→ multiplicación de potencias de igual base
Se obtiene:
Luego:
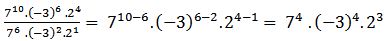→ división de potencias de igual base
Se resuelven las potencias posibles:
Se resuelve la multiplicación de números enteros
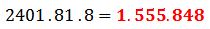
Ejercicio 4
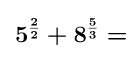
Se aplican las propiedades de la potencia necesarias:
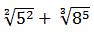→ potencia de exponente racional
Se resuelven las potencias posibles:
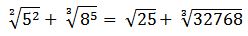
Se resuelven las raíces:
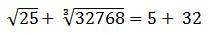
Se resuelven las sumas:
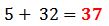
Ejercicio 5
Se resuelven las potencias posibles:
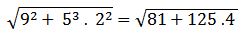
Se resuelven las multiplicaciones y las sumas:
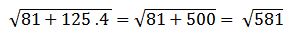
Se resuelve la raíz:
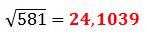
Ejercicio 6
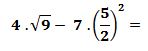
Se resuelve la raíz:
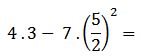
Se resuelven las potencias posibles:
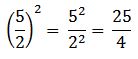
Quedando la operación de la siguiente manera:
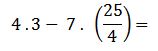
Se resuelven las multiplicaciones:
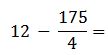
Se resuelve la resta de fracciones:
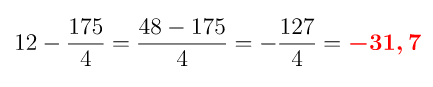
Ejercicio 7
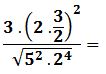
Se resuelven las potencias posibles:
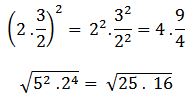
Quedando la operación de la siguiente manera:
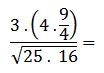
Se resuelven las multiplicaciones:
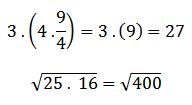
Quedando la operación de la siguiente manera:
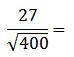
Se resuelve la raíz:
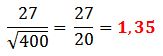
Ejercicio 8
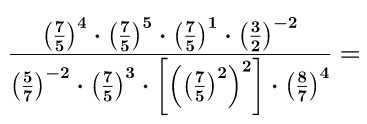
Se resuelven las potencias posibles:
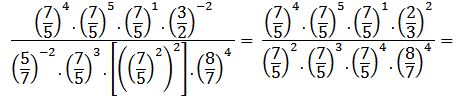
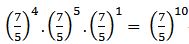→ multiplicación de potencias de igual base
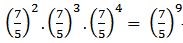→ multiplicación de potencias de igual base
Quedando la operación de la siguiente manera:
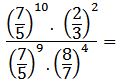
Luego:
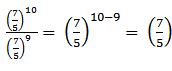→ división de potencias de igual base
Quedando la operación de la siguiente manera:
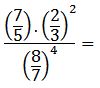
Se resuelven las potencias posibles:
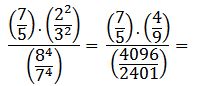
Se resuelven las multiplicaciones:
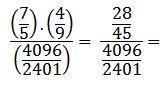
Se resuelve la división:
¿Sabías qué…?
Toda potencia de base negativa con exponente “par” da como resultado un número positivo. Por ejemplo:
Toda potencia de base negativa con exponente “impar” da como resultado un número negativo. Por ejemplo:
Para practicar:
