VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
El triángulo es una de las figuras más estudiada en la geometría. Aunque es el polígono más simple, sus características únicas han permitido que tenga relevancia en otras ciencias. En este artículo aprenderemos a construir las rectas y los puntos notables del mismo.
Triángulo
Es el resultado de unir tres puntos de un plano con líneas rectas. Un triángulo es un polígono formado por tres segmentos y se caracteriza porque la suma de sus tres ángulos interiores es igual a 180 °.

Otro nombre empleado para referirse a este polígono es “trígono” aunque es un término poco usado.
Clasificación de los triángulos
Existen varios criterios de clasificación que permiten agrupar a los triángulos de acuerdo a ciertas particularidades: según la medida de sus lados y según la medida de sus ángulos.
- Según la medida de sus lados
- Según la medida de sus ángulos

Clasificación de los ángulos.
Otro criterio de clasificación
Existe otro criterio de clasificación que considera los ejes de simetría que tenga un triángulo, el cual puede tener un solo eje de simetría, más de un eje de simetría o ningún eje de simetría.

Clasificación de los triángulos según sus ejes de simetría.
Rectas notables
La mediatriz, la mediana, la altura y la bisectriz son las rectas notables de los triángulos. Cada triángulo presenta tres de cada una.
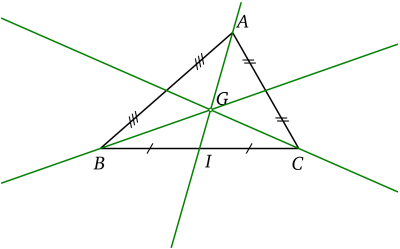
Sin importar el tipo de triángulo que sea, las tres medianas de un ángulo son interiores.
Alturas según el tipo de triángulo
Según el tipo de triángulo, sus alturas pueden presentar características especiales. Por ejemplo, en los triángulos rectángulos, dos de sus alturas coinciden con sus dos catetos, la altura respecto a la hipotenusa es la única altura interior. En los acutángulos, todas las alturas son interiores. Por su parte, en el caso de los trángulos obtusángulos, solamente la altura respecto a su lado mayor es interior.
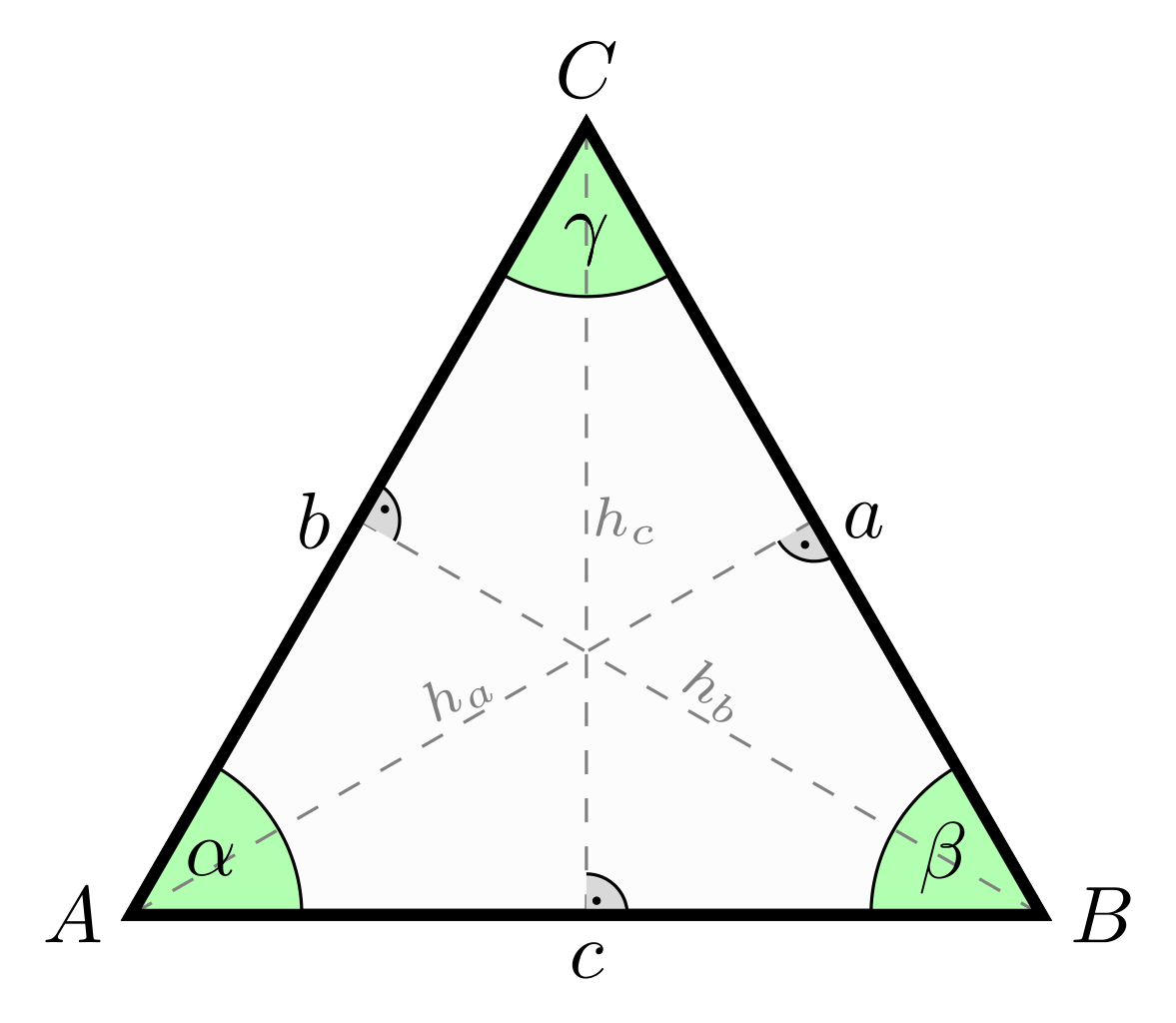
La altura de un triángulo isósceles correspondiente al lado desigual divide al triángulo en otros dos triángulos de igual área.
Fuente: https://commons.wikimedia.org/wiki/User:MartinThoma
¿Sabías qué?
En los triángulos equiláteros coinciden todas las rectas y puntos notables.
Puntos notables en los triángulos
Sin importar el tipo de triángulo, sus puntos notables son cuatro: baricentro, ortocentro, circuncentro e incentro. Todos ellos son el resultado de la intersección de rectas notables.
Baricentro: corresponde al punto en donde se intersecan las medianas de un triángulo.
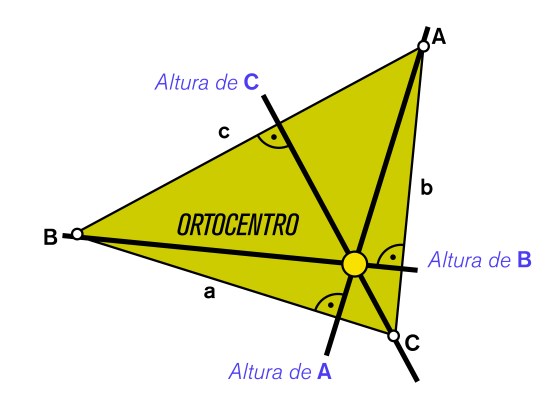
Ortocentro: es aquel punto en el que se cortan las alturas de un triángulo.
Circuncentro: se forma en el punto de intersección de las mediatrices de un triángulo. En el caso de los triángulos obtusángulos, el circuncentro se encuentra fuera del triángulo.
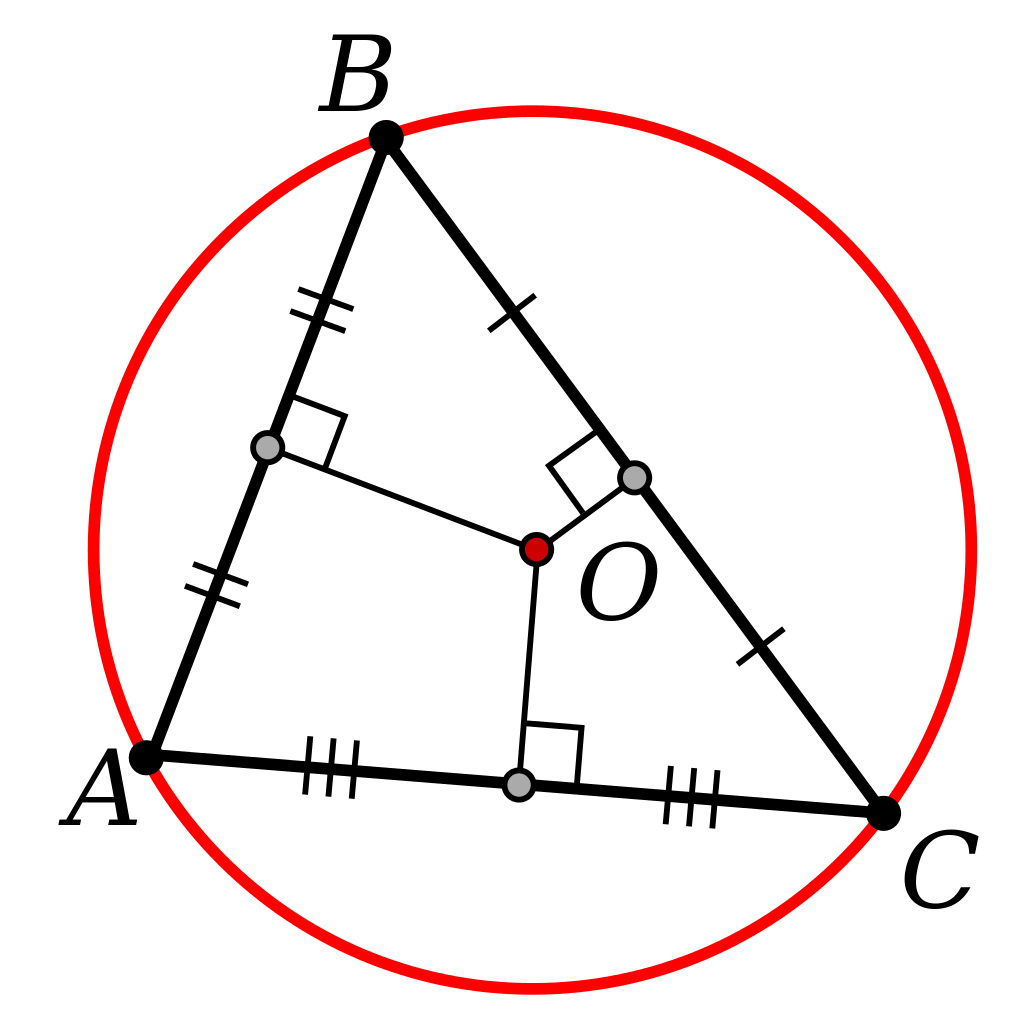
El circuncentro representa el centro de la circunferencia circunscrita de un triángulo.
Incentro: es el punto en el que todas las bisectrices de un triángulo concurren.
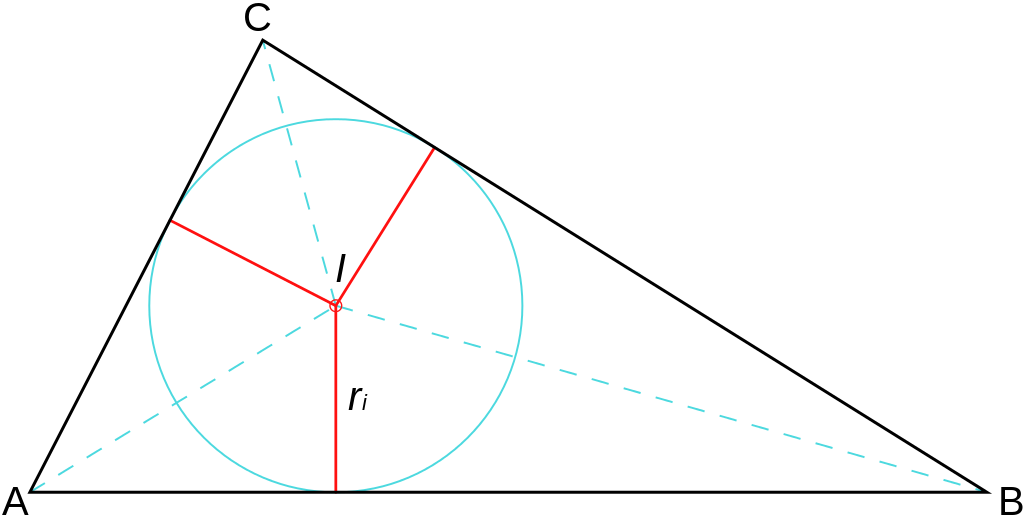
El incentro corresponde al centro de la circunferencia inscrita dentro del triángulo.
Construcción de rectas y puntos notables
Para trazar una mediana habrá que unir el punto medio de un lado del triángulo con el vértice opuesto. El punto en donde se cortan las tres medianas corresponderá al baricentro.

Para trazar la bisectriz de un vértice se debe pinchar con el compás en el mismo y abrirlo en cualquier medida. Luego se traza un arco que corte los dos lados del triángulo en los puntos 1 y 2. Posteriormente se selecciona una abertura del compás que sea un poco mayor que el arco trazado y luego con dicha abertura se traza un arco desde 1 y otro desde 2.
El corte de los dos últimos arcos corresponderá al punto 3. Para obtener la bisectriz solo se debe unir el vértice seleccionado anteriormente con el punto 3.
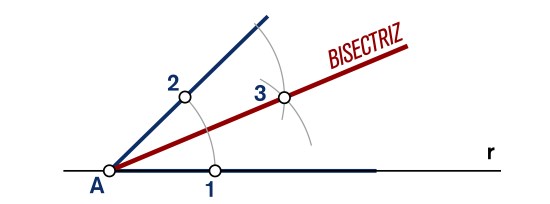
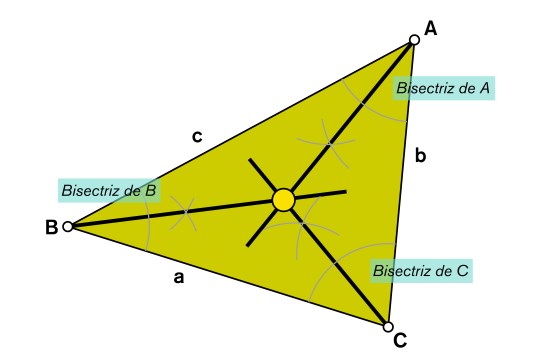
Seleccionando los otros dos vértices y aplicando el mismo procedimiento anterior se podrán trazar las bisectrices restantes. El corte de todas las bisectrices corresponderá al incentro.
Por medio de una escuadra se ubica el ángulo recto sobre el lado que se desea trazar la altura de manera que la recta marcada pase por el vértice opuesto a dicho lado.
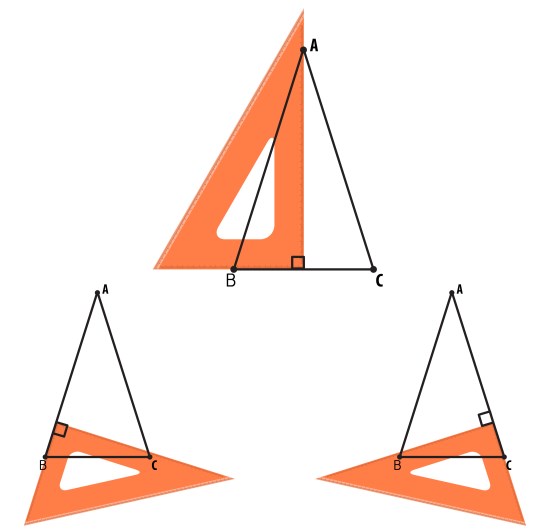
Una vez trazadas todas las alturas, el punto donde éstas se cortan corresponde al ortocentro.
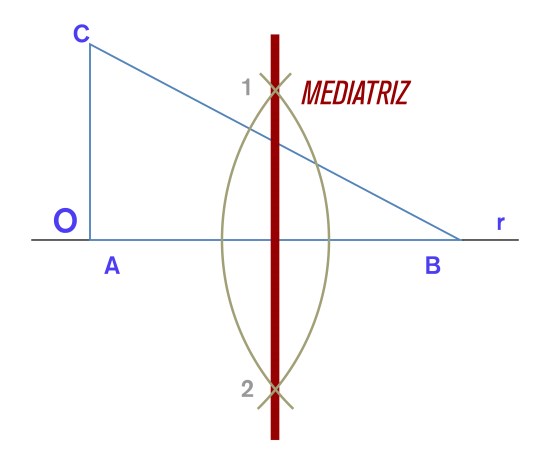
Mediatriz y circuncentro
Para trazar la mediatriz que pasa por uno de los lados del triángulo se debe seleccionar una abertura del compás, luego pinchar uno de los vértices comunes con dicho lado y trazar un arco. Repetir el procedimiento en el otro vértice con la misma abertura de compás y unir los cortes de los dos arcos trazados. La recta resultante corresponderá a la mediatriz del triángulo respecto al lado escogido.
Luego de trazar las mediatrices de los demás lados del triángulo, el punto de corte de las mismas corresponderá al circuncentro.