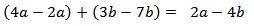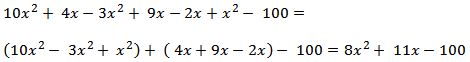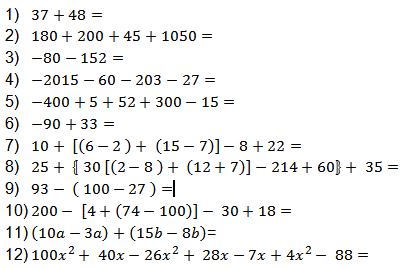LEY DE LOS SIGNOS: SUMA Y RESTA

Dentro de la matemática existen distintos tipos de operaciones con sus respectivos procedimientos. Las operaciones combinadas deben resolverse empleando una serie de leyes y propiedades basadas en los signos de los números.
Las operaciones combinadas son expresiones formadas por números que se agrupan de diferentes formas en operaciones diversas. Estas operaciones pueden emplear símbolos como paréntesis, corchetes y llaves, los cuales se encargan de unir un grupo de números.
Para resolver las operaciones combinadas se debe tener en cuenta:
- Para sumar o restar dos números, ambos deben estar sueltos, es decir, no se pueden sumar o restar dos números si uno de ellos está unido a otra expresión mediante un símbolo u otro signo como el de la multiplicación.
- Los signos de multiplicar generan una unión más fuerte que los de sumar y restar, es decir, cuando dos o más números están unidos por un signo de multiplicación generan una unión inseparable, mientras que los que están unidos por signos de suma y resta se encuentran más sueltos en la operación.
- Las operaciones combinadas deben resolverse utilizando los pasos correspondientes, es decir, todo lo que se resuelve en un paso debe copiarse, sin realizar cambios, al inicio del siguiente paso.
- Antes de comenzar a resolver las operaciones combinadas se deben conocer las propiedades de dichas operaciones, para así plantear una estrategia a seguir sin cometer errores.
- Siempre se resuelve primero lo que está en el interior del paréntesis o de cualquier otro signo, para seguir luego con las multiplicaciones y finalmente con las sumas y restas.
Ley de los signos en suma y resta
- Cuando los números a operar son positivos, se suman y se conserva el signo positivo.
Ejemplo 1
25 + 30 = 55
Ejemplo 2
100 + 250 + 375 + 2000 = 2725
- Cuando los números a operar son negativos, se suman y se conserva el signo negativo.
Ejemplo 1
- 42 - 182= - 224
Ejemplo 2
- 3025 - 560 - 104 - 37 = - 3726
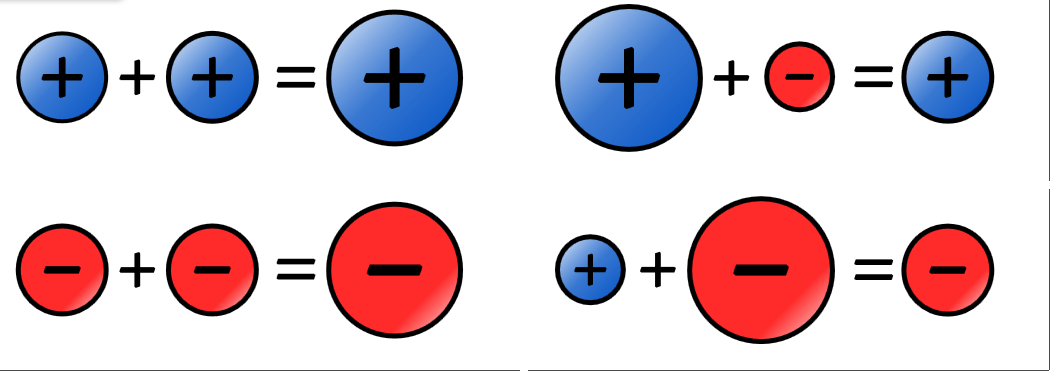
Símbolos de la ley de los signos.
- Cuando los números a operar son de diferente signo, se restan y se coloca el signo del número mayor.
Si en la operación hay varios números positivos y varios números negativos, se utilizan las reglas para resolver operaciones combinadas:
- Se suman los números que tengan signos iguales. Por ejemplo:
- 487 + 55 + 12 + 100 - 13 =
- 487 - 13 = -500
55 + 12 + 100 = 167
- Se restan ambos resultados obteniendo un número final y se coloca el signo del número mayor.
- 487 + 55 + 12 + 100 - 13 = - 500 + 167 = - 333
Ejemplo 1
- 117 + 43 = - 74
Ejemplo 2
200 - 160 - 65 + 328 = 528 - 225 = 303
- Cuando hay un paréntesis, llave o corchete, se resuelve primero lo que está dentro de estos símbolos antes de efectuar cualquier otra operación. El orden para resolver dichos símbolos es el siguiente: primero los paréntesis, luego los corchetes y finalmente las llaves.
Ejemplo 1
2 + [(4 - 2) + (4 - 7)] - 10 + 25 = 2 + [2 - 3] – 10 + 25
= 2 - 1 - 10 + 25 = -11 + 27 = 16
Ejemplo 2
Paso 1: 10 + {[20[(2 - 5) + (5 + 7)] - 118 + 20]} + 46 = 10 + {[20[-3 + 12] - 118 + 20]} + 46
Paso 2: 10 + {[20[-3 + 12] - 118 + 20]} + 46 = 10 + {20[9] - 118 + 20} + 46 = 10 + {180 - 118 + 20} 46
Paso 3: 10 + {180 - 118 + 20} + 46 = 10 + 82 + 46
Paso 4: 10 + 82 + 46 = 138
- Si hay un signo negativo delante de un paréntesis, corchete o llave, los números que se encuentren dentro de estos símbolos cambian inmediatamente su signo. Si el signo es positivo, todo se mantiene igual.
Ejemplo 1
64 - ( 35 - 10 ) = 64 + (- 35 + 10) = 64 - 25 = 39
Ejemplo 2
100 - [2 + (98 - 120)] - 15 + 3 = 100 + [- 2 - 98 + 120] - 15 + 3 =
100 + [- 100 + 120] - 15 + 3 = 100+20 - 15 + 3 = 123 - 15 = 108
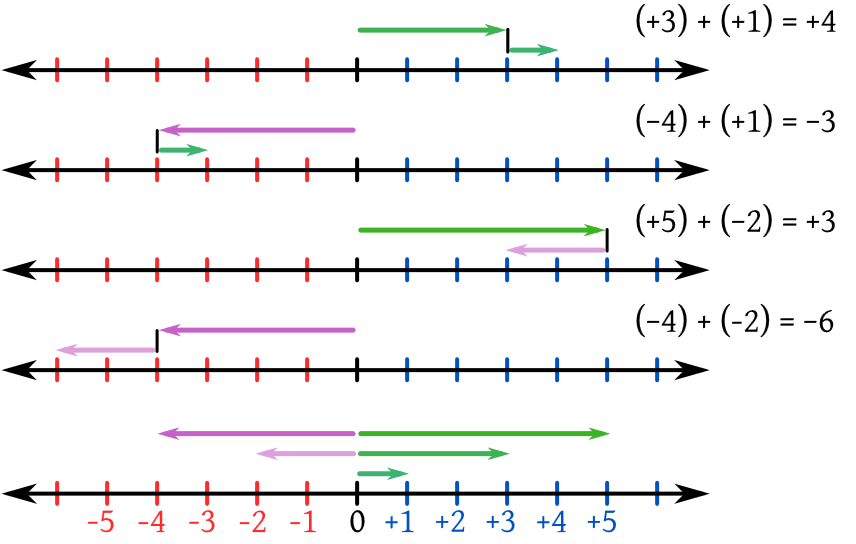
Interpretación gráfica de la ley de los signos.
Propiedades de los signos en las operaciones algebraicas
- Suma algebraica: esta operación tiene como objetivo unir dos o más sumandos en una única expresión conocida como suma o adición. Para que una suma algebraica esté totalmente completa, los términos semejantes entre los sumandos deben estar simplificados en su totalidad.
- Resta algebraica: esta operación se realiza de manera similar a la suma algebraica, pero en vez de sumar términos semejantes, se restan dichos términos hasta estar simplificados en su totalidad.
La regla general para resolver una suma o resta algebraica es la siguiente:
“Signos iguales se suman, signos diferentes se restan, agrupando los términos semejantes ya sean letras o exponentes”.
Ejemplo 1
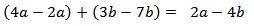
Ejemplo 2
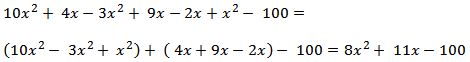
Hasta este paso se simplificaron en su totalidad todos los términos semejantes, luego de este paso, se efectúa un procedimiento diferente conocido como ecuación cuadrática que será estudiado más adelante.
Para practicar
Resuelve las siguientes operaciones combinadas:
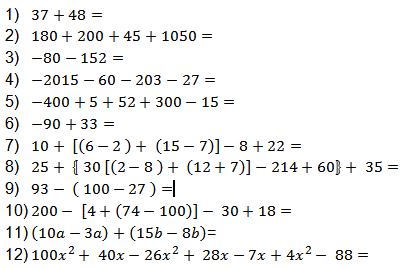
 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS