 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
La geometría analítica
Permite representar a las figuras geométricas usando técnicas básicas del análisis de un sistema de coordenadas.
¿Sabías qué?
La pendiente es el parámetro principal en la construcción de carreteras, conductos y otros elementos donde el suelo tenga algún desnivel.
Vectores en el plano
Son segmentos de rectas orientados en el plano (x,y) y constan de módulo, dirección y un sentido determinado.
¿Sabías qué?
La ecuación de la recta permite definir la relación de costos, inversión y ganancias en la microeconomía de una empresa.
La ecuación de la recta está involucrada profundamente en nuestro día a día. Posee variadas aplicaciones, como describir la posición, el movimiento y la inclinación de un terreno; también es de gran utilidad en economía, para analizar distintas variables. Estos son algunos de los usos de la función lineal. Aprende todo sobre ella a continuación.

Una recta es una línea que no posee ni principio ni fin. Sin embargo, la ecuación de la recta tiene variadas aplicaciones en cálculos concretos, como las distancias.
La ecuación de la recta es una expresión algebraica que describe una línea recta, relacionando la variación de y con respecto a x, la cual puede ser graficada en el plano cartesiano según los componentes en cada uno de los ejes.
PLANO CARTESIANO
Para comprender con precisión todos los parámetros que involucra la ecuación de recta, es necesario entender qué es el plano cartesiano y cada una de sus partes fundamentales.
El plano cartesiano consiste en dos rectas perpendiculares que se cortan en un punto, esta intersección se conoce como origen. La línea horizontal indica los valores de las abscisas y se denota con la letra x, mientras que el eje vertical corresponde a las ordenadas y se identifica con la letra y.
Cuadrantes
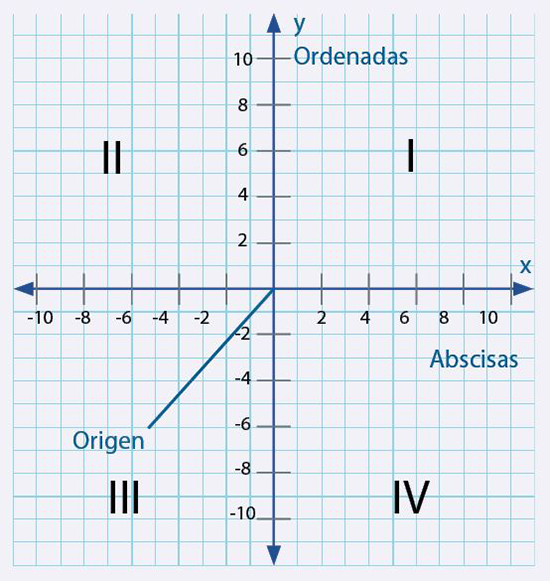
El plano cartesiano está dividido en cuatro cuadrantes, numerados en sentido contrario a las manecillas del reloj.
En el cuadrante I: ambas coordenadas (x,y) son positivas.
En el cuadrante II, la coordenada en x es negativa, mientras que la coordenada y es positiva.
En el cuadrante III ambas coordenadas tienen valores negativos.
Mientras que en el cuadrante IV, la coordenada x es positiva pero y es negativa.
PUNTOS
Todo punto A, en la gráfica, tendrá un par ordenado con componentes tanto en el eje de las abscisas como en el eje de las ordenadas. Se expresa de la siguiente forma: A (x,y).
Por lo tanto, para ubicar un punto en el plano cartesiano, debemos trazar una recta perpendicular al eje de las x, que pase por la abscisa x; luego se traza una recta perpendicular al eje y, que pase por la ordenada y.

El punto A (4,3) se ubica en la intersección entre las rectas: y = 3 y x = 4.
RESOLVAMOS LOS SIGUIENTES EJERCICIOS:
Ubicar en el plano cartesiano los puntos:
A = (4, 2)
B = (2, 6)
C = (−2, 4)
Intenta tú:
D = (3, 7)
E = (5, −1)
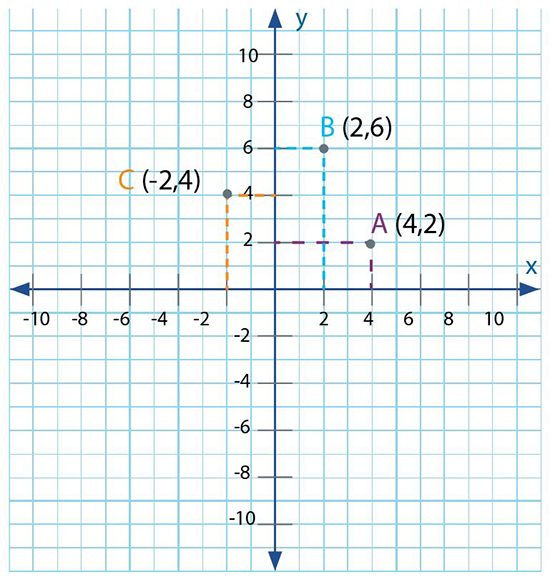
Ubica los puntos D y E. Recuerda que el primer número corresponde al eje de las abscisas (x) mientras que el segundo corresponde al eje ordenadas (y).

Un plano se determina mediante ejes cartesianos. La unión de una calle con una avenida es una intersección.
Ahora bien, cuando entramos en el mundo de las funciones matemáticas, podemos relacionar todo lo que nos rodea con la intersección de dos rectas, y utilizar un plano cartesiano para describir la relación entre ambos ejes.
DESCARTES Y EL PLANO CARTESIANO

El plano cartesiano tiene dicho nombre en honor a René Descartes, filósofo, matemático y científico francés. Quien estableció en su pensamiento filosófico la necesidad de tomar un punto de partida sobre el cual edificar el conocimiento. En su faceta de matemático creó la geometría analítica, la cual incorpora el trazo de dos rectas perpendiculares entre sí, con un punto de intersección denominado origen. Así nacen las coordenadas cartesianas.
UBICACIÓN EN EL PLANO

Relación calle- avenida en las esquinas de la ciudad. La ubicación de puntos en el plano no es simplemente un aspecto de la matemática teórica, puede ser aplicada a la vida cotidiana.
Por ejemplo, si deseas dirigirte a un lugar determinado, sea cual sea, necesitas conocer la dirección. Las intersecciones entre calles nos orientan cuando deseamos ubicar una dirección en particular.

En un plano de ciudad, tanto las abscisas como las ordenadas corresponden a calles y algunas avenidas.
ECUACIÓN LINEAL
La ecuación de la línea recta tiene una forma general y es:
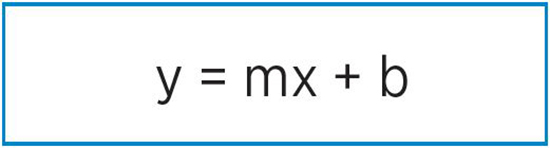
Donde: y define el eje de las ordenadas y comprende a las variables independientes; x representa el eje de las abscisas, que incluye a las variables independientes; m es la pendiente de la recta y b hace referencia al punto de intersección de la recta con el eje y.
¿QUÉ ES LA PENDIENTE?
El ciclismo de aventura
Es un deporte extremo que brinda múltiples beneficios, tanto físicos como mentales, fortalece el cuerpo, la concentración y mejora el control mental. La mayoría de las veces, durante la trayectoria, se requiere utilizar el freno trasero, pues al descender por una pendiente elevada si se frena con el delantero el ciclista saldrá expulsado hacia adelante.

La pendiente está relacionada con el ángulo de inclinación de una recta. Es un término utilizado para describir una de las características de un terreno.
La pendiente (m) es un número que define el grado de inclinación que posee la línea recta, esta puede ser de diferentes maneras de acuerdo a ciertas condiciones.
Si m es un número menor que cero, la pendiente es negativa y por lo tanto la recta será descendente.
Si m es un número mayor que cero, la pendiente es positiva y por lo tanto la recta será ascendente.
Mientras que si m es igual a cero, no hay pendiente, es decir, tendremos una recta horizontal paralela al eje de las y.
Como la pendiente es la relación existente entre cada uno de los ejes, es posible determinar el grado de inclinación entre dos puntos conocidos usando una transformación de la ecuación principal de la recta. Tal como se muestra en la siguiente fórmula:

Donde:
x1 e y1 pertenecen al punto P1 y x2 e y2 pertenecen al punto P2.
ORDENADA AL ORIGEN
En cuanto al punto de intersección (b), es el punto de corte con el eje y cuando la variable independiente x es igual a cero. Entonces, cuando el punto de intersección u ordenada al origen es igual a cero, la recta pasa por el punto (0,0) que es el origen.
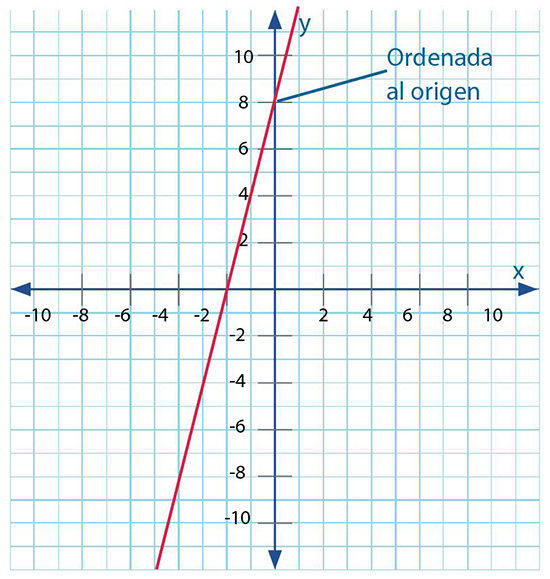
Veamos un ejemplo práctico:
Dada la ecuación de la recta:
y = 2x + 3
La pendiente es 2 y el punto de intersección de la recta con el eje y es igual a 3. Para determinar el valor de y es necesario darle valores a x y efectuar la operación correspondiente. De la siguiente manera:
Si x = 1
y = 2•(1) + 3
y = 2 + 3
y = 5
Por lo tanto, el primer punto en la recta que satisface la ecuación es (1, 5).
Si x = 2
y = 2•(2) + 3
y = 4 + 3
y = 7
Por lo tanto, el segundo punto en la recta que satisface la ecuación es (2, 7).
De la misma forma asignamos otros valores a la variable independiente x para determinar otros valores de la variable dependiente y, y de esta forma trazar la recta de la ecuación. Para obtener una recta bien definida te recomendamos utilizar al menos tres puntos. Con dos puntos pertenecientes a la recta ya es posible trazarla, pero para evitar errores procedimentales al realizar los cálculos, es conveniente buscar más de dos puntos.
Hallamos dos puntos más:
x = -1, y = 1
x = -2, y = -1
Ahora procedemos a graficar los 4 puntos que hemos determinado.
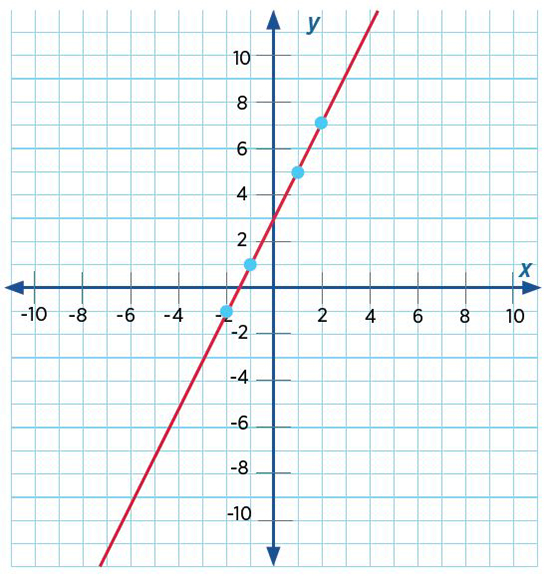
El punto de intersección se determina analíticamente de la siguiente manera:
Cuando x = 0
y = 0•(2) + 3
y = 3
Para hallar la pendiente, reemplazamos dos de los puntos en la ecuación:
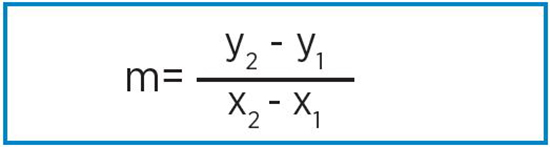
A (1, 5)
B (2, 7)
Y obtenemos:
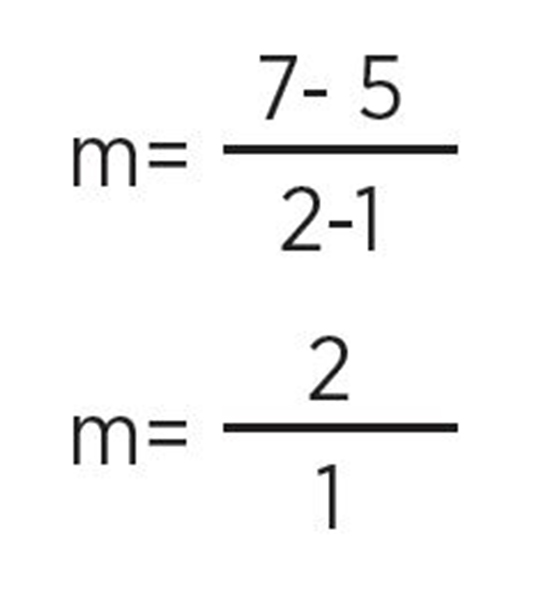
El grado de inclinación o pendiente de la recta m es igual a 2.
APLICACIONES
Un gran número de actividades cotidianas están representadas por una función lineal, por lo que es posible relacionarlas con la ecuación de recta.
Además del movimiento, podemos relacionar a la ecuación de la recta con algo tan sencillo como la compra del pan para la cena, pues en muchos de los casos esta actividad está descrita por una función lineal. Por ejemplo: Si cada una de las personas de una casa come 3 panes diariamente en la cena y adicionalmente compran 4 panes para el día siguiente. Tenemos una función representada en la siguiente ecuación:
y = 3x + 4
Donde y representa a la función y x corresponde a las personas que estarán presentes a la hora de la cena. ¿Podrías graficar la función correspondiente?