 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
FUNCIÓN EXPONENCIAL EN FÍSICA
En las carreras de Fórmula 1 se puede observar las aceleraciones de velocidad de forma exponencial, cada segundo aumentan la velocidad en mayor proporción dados sus potentes motores.
¿Sabías qué?
En algunos países en el mundo se limita la utilización del interés compuesto, ya que puede crear deudas que se hacen impagables.
LEY DE DECAIMIENTO EXPONENCIAL
Una sustancia radiactiva tiene un ritmo de desintegración, que se produce de acuerdo a la función N (t) = N0e -λt.
¿Sabías qué?
Todas las herramientas matemáticas tienen aplicación en cálculos cotidianos, lo que les da sentido a su existencia.
La función exponencial tiene variadas aplicaciones: en interés compuesto, crecimiento de poblaciones y desinte- gración radiactiva, entre otras. Es por ello que es una de las más utilizadas. ¡Conozcamos más acerca de ella!

Lo primero que necesitamos saber antes de interiorizarnos en todo lo que respecta a función exponencial es saber qué es una función y de qué está compuesta.
Función: Es la correspondencia entre los elementos de un conjunto de salida o dominio con los elementos pertenecientes al conjunto de llegada o codominio. Comúnmente estos conjuntos suelen relacionarse por medio de ecuaciones, en las cuales se indica cómo obtener valores de y a partir de x. Estos valores pueden ser representados en una gráfica.
Variables: son elementos relacionados que indican un comportamiento y definen una función.
FUNCIÓN EXPONENCIAL
Es una función definida por la forma f(x) = k.ax, donde la variable x determina el crecimiento o decrecimiento continuo y acelerado de una variable, a es un número perteneciente a los números reales positivos diferente de 1 y k es un número real distinto de 0.
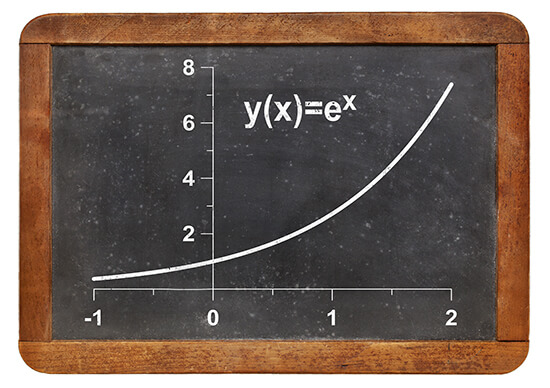
La función exponencial se representa en una curva que puede ser de crecimiento (como en la imagen) o disminución continua acelerada.
PROPIEDADES DE LA FUNCIÓN EXPONENCIAL CON K=1
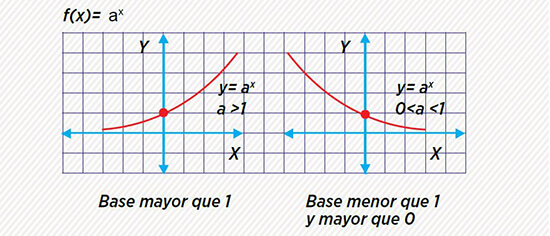
Ejemplos
Esta función está bien definida en todos los números reales, veamos cómo se aplica en el caso f(x) = 3x. Si se le dan valores sucesivos desde 0 hasta 4 positivo se verán los siguientes resultados.
30=1, 31=3, 32=9, 33=27, 34=81
|
f |
0 |
1 |
2 |
3 |
4 |
|
f(x) |
1 |
3 |
9 |
27 |
81 |
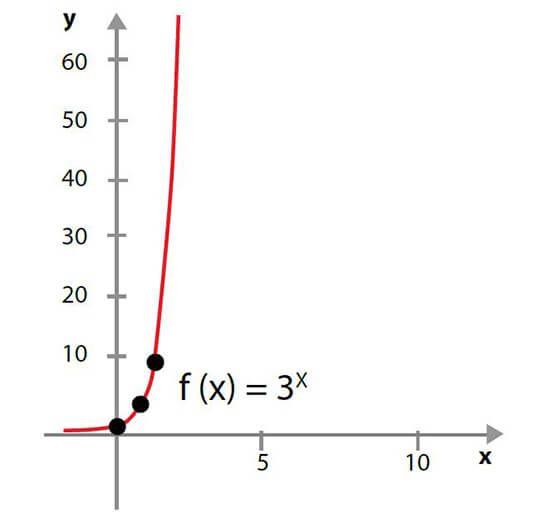
En la gráfica aproximada se ve el crecimiento exponencial o acelerado y esto se debe a que la base es mayor a 1.
Como se mencionó en las propiedades, la función exponencial solo es aplicable cuando la base es positiva, porque con bases negativas la función no tendría imágenes en los números reales.
De esta forma (-3)x no podría colocarse como función exponencial, para observar la afirmación se le dará los valores de 1, 2, y 3 a la variable, y se presentan los siguientes resultados:
(-3)1 = -3, luego (-3)2 = 9, y después (-3)3 = -27. Así se da un valor positivo (9) en medio de 2 soluciones negativas, anulando todo sentido exponencial en la función.
APLICACIONES DE LA FUNCIÓN EXPONENCIAL
En finanzas
En el interés compuesto se utiliza la función exponencial para resolver cuestiones referidas al manejo del dinero.

En una de las ramas de la economía, las finanzas, las matemáticas son fundamentales.
Si la base tiene algún valor entre 0 y 1, es decir cuando la base es una fracción, la función decrecerá en forma continua.
Así por ejemplo, si se estudia la función:
f(x) = (1/3)x, y se le dan valores de 1, 2, y 3 a la variable, se tendrá como resultado:
(1/3)1 = 1/3, (1/3)2 = 1/9, (1/3)3 = 1/27, (1/3)4 = 81
Estos resultados se representan en la siguiente tabla:
|
f |
1 |
2 |
3 |
4 |
|
f(x) |
1/3 |
1/9 |
1/27 |
1/81 |
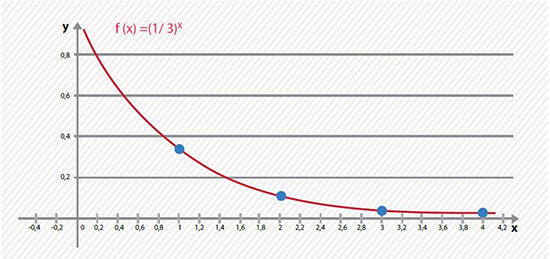
Al dibujar una gráfica exponencial manualmente, se deben ubicar algunos puntos y en base a ellos se traza la curva aproximada de la función.

El dinero escondido que solo alcanzarás con una inversión es la ganancia.
INTERÉS
El interés es la ganancia sobre un préstamo, depósito o inversión, y se obtiene al multiplicar éste por algún porcentaje o tasa. De esta forma, si la tasa de interés es de 30%, el interés de 200 unidades será 60 unidades.
El interés compuesto es una clase de interés que se caracteriza por generar ganancia en sí mismo, se conoce también como interés sobre interés.
FÓRMULA Y FACTORES DE CÁLCULO EN EL INTERÉS COMPUESTO
La fórmula general para determinar el interés compuesto es:
F = P (1 + i)n
De la cual se tienen los siguientes términos:
F: Es el valor final o futuro de un depósito o deuda después de aplicada una tasa de interés durante un tiempo.
P: Es el valor presente de un depósito o préstamo.
i: Es la tasa de interés aplicada expresada en términos decimales, provenientes de la expresión en números naturales de un porcentaje.
n: Es el tiempo referido en la operación.
Ejemplo
Si se prestan 200 unidades de cualquier moneda con un interés anual compuesto del 20% durante 3 años. Calcular el valor final.
Al separar los datos resulta:
P = 200 unidades
i = 20% = 0,20
n = 3 años
Se sustituye cada uno de los términos en la fórmula:
F = 200 (1 + 0,20)3 = 345,6

El interés compuesto es una acumulación de intereses a partir de un capital inicial.
Así las 200 unidades se trasforman en 345,6 unidades.
Se podría decir que esto no permite ver el crecimiento exponencial, pero si se ve el progreso veremos cómo:
En un año pasa de 200 a 240, creciendo en 40 unidades que son el 20% de 200.
Para el segundo año de 240 a 288, creciendo en 48 unidades, que son el 20% de 240 y no de 200.
Para el tercer año el crecimiento será el 20% de 288, que resulta en 57,6 y llega a 345,6.
El crecimiento es exponencial porque cada vez es mayor, si el crecimiento fuera igual período a período resultaría proporcional.
ESTADÍSTICAS POBLACIONALES
Las estadísticas poblacionales se refieren al número de individuos con una misma característica, y sus variaciones (aumento o disminución).
Para la proyección de crecimiento poblacional o una disminución poblacional se aplica la misma fórmula de interés compuesto cambiando el parámetro principal. Ahora no se utilizará tasa de interés sino tasa de crecimiento o de disminución.

El crecimiento poblacional puede expresarse en funciones exponenciales.
DISMINUCIÓN POBLACIONAL
Para calcular la disminución poblacional se requiere hacer uso de la función exponencial. Veamos un ejemplo:
Se ha establecido que la población de la tercera edad a nivel mundial disminuye en un 15% anual, y que hoy en día existe un aproximado de 1.000 millones de personas con esa condición. ¿Cuántas personas de la tercera edad aproximadamente existirán en 4 años?
Si se resuelve progresivamente se observara mejor la disminución exponencial.
De esta forma 1.000 por el 15% son 150, por lo cual si restamos en el primer año el número de personas en la tercera edad pasara de 1.000 millones a 850 millones.
Aplicando el mismo cálculo para los años sucesivos resultará:
En el segundo año una reducción de 127,5; pasa de 850 a 722,5 millones de personas.
Para el tercer año se da una baja de 108,38; al ir de 722,5 a 614,12 millones.
En el cuarto año la población habría disminuido aproximadamente a 522 millones de personas, acercándose a la mitad de la población inicial.

La especie Nymphaea nouchali habita en ciertas regiones de Asia, puede soportar aguas contaminadas.
CRECIEMIENTO DE PLANTAS
Los nenúfares son un tipo de plantas acuáticas que resaltan por su belleza y sus diversas funciones en el ecosistema. En los lugares dónde se encuentra este tipo de plantas se sabe que la superficie que cubren se duplica cada día. ¿Cuál será la superficie ocupada por éstas plantas dentro de 10 días si en el momento del análisis, la superficie era de 1 m2?
En este problema, cuando se menciona que la superficie ocupada por nenúfares “duplica cada día” se hace mención a una función exponencial que puede expresarse de esta forma:
f(x) = 2x
De donde:
f(x): Es la superficie ocupada por los nenúfares en metros cuadrados.
x: Es el número de días.
Quiere decir que para determinar la superficie ocupada por estas plantas acuáticas bastará por sustituir 10 en la variable x de la siguiente forma:
f(10) = 210
De manera que f(10) = 1024
En 10 días la superficie ocupada por nenúfares será de 1024 m².