 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
Los Subíndices
Los subíndices de una sucesión no siempre comienzan desde el número 1, por ejemplo en las ciencias de la computación se emplean sucesiones que inician desde cero y usan variables diferentes a n.
¿Sabías qué?
Las sucesiones matemáticas son una aplicación de los números naturales en los números reales.
UN APORTE INCALCULABLE
Fibonacci llevó a Europa el sistema de numeración indoarábico donde se usaban los números hindúes (1, 2, 3...) y el 0 árabe, lo que simplificó los cálculos que en la época se hacían con números romanos.
¿Sabías qué?
Los términos de una sucesión de Fibonacci se conocen como “números de Fibonacci” y guardan mucha relación con varios elementos de la naturaleza.
La manera en la que ordenamos los números y contamos de dos en dos, son algunos de los ejemplos de sucesiones matemáticas. Ellas han sido objeto de estudio desde hace muchos años debido a sus diversas aplicaciones, incluso su principio puede ser observado en la naturaleza y otras situaciones.

SUCESIONES
Una sucesión es un conjunto ordenado de elementos que comúnmente son números (a1, a2, a3, a4, a5, a6, a7, a8…), donde cada uno de ellos, denominados términos, puede calcularse a partir de cierto criterio conocido como regla de formación.
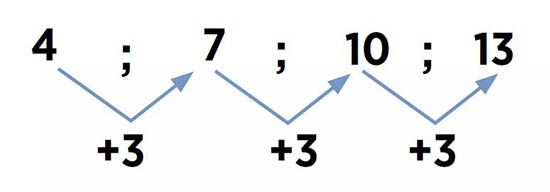
Si sumamos 3 a cada término de la sucesión mostrada se tiene como resultado el valor del término siguiente. Esta propiedad que tienen las sucesiones se conoce como regla de formación.
Muchas veces el número de términos de una sucesión es infinito. Sin embargo, se denomina longitud de la sucesión al número de términos pertenecientes a éste.

Una sucesión matemática es un conjunto ordenado de términos que se pueden determinar a través de cierto criterio.
NOTACIÓN
La notación más común para expresar las sucesiones emplea la forma (an), en donde el término an representa al elemento que se encuentra en la posición n de la sucesión (también se conoce como término n-ésimo en el que n puede ser cualquier número positivo).
Por ejemplo, la sucesión de los números impares positivos se puede expresar como:
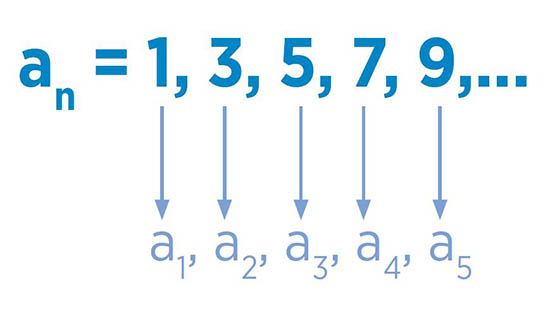
an = 1, 3, 5, 7, 9,…
Los términos en una sucesión suelen expresarse con subíndices que indican la posición de estos en la sucesión.
an = a1, a2, a3, a4, a5,…
Del ejemplo anterior se tiene que:
LA FORMA GENERAL DE LAS SUCESIONES
Las sucesiones matemáticas pueden expresarse en un término o forma general para el caso en el que sus elementos queden determinados por la regla de formación. En el caso del ejemplo de los números impares pueden expresarse mediante la forma general:
an = 2n – 1
Cada elemento de esta sucesión puede obtenerse al sustituir el valor n por el número de posición del término que se desea hallar. De este modo se tiene:
| Valor de n | Sustitución en la forma general: | Término |
|---|---|---|
|
n = 1 |
a1 = 2n – 1 = 2(1) – 1 = 1 |
Primer término |
|
n = 2 |
a2 = 2n – 1 = 2(2) – 1 = 3 |
Segundo término |
|
n = 3 |
a3 = 2n – 1 = 2(3) – 1 = 5 |
Tercer término |
|
n = 4 |
a4 = 2n – 1 = 2(4) – 1 = 7 |
Cuarto término |
|
n = 5 |
a5 = 2n – 1 = 2(5) – 1 = 9 |
Quinto término |
Algunos ejemplos de sucesiones particulares
| Forma general | Representación de la sucesión |
|---|---|
|
an= 2n |
Números pares (2, 4, 6, 8,…) |
|
an = 2n – 1 |
Números impares (1, 3, 5, 7,…) |
|
an = n2 |
Potencias cuadradas (1, 4, 9, 16,…) |
|
an = n3 |
Potencias cúbicas (1, 8, 27, 64,…) |
|
an = (-1)n |
-1, 1, -1, -1,… |
|
an = (-1)n+1 = (-1)n-1 |
1, -1, 1, -1, 1,… |
HAGAMOS UN EJERCICIO
Determina los primeros 5 términos de la sucesión de los números pares positivos empleando su forma general.
Procedimiento:
• Los números pares cumplen con el principio de que el valor de un término es el doble del término anterior, la forma general es:
an = 2n
• Para determinar los primeros 5 términos de la sucesión solo se deben sustituir el número de posición de cada término en n:
| Valor de n | Sustitución en la forma general: | Término |
|---|---|---|
|
n = 1 |
a1 = 2n = 2(1) = 2 |
Primer término |
|
n = 2 |
a2 = 2n = 2(2) = 4 |
Segundo término |
|
n = 3 |
a3 = 2n = 2(3) = 6 |
Tercer término |
|
n = 4 |
a4 = 2n = 2(4) = 8 |
Cuarto término |
|
n = 5 |
a5 = 2n = 2(5) = 10 |
Quinto término |
• De esta manera se tienen los primeros cinco términos de la ecuación:
a1 = 2, a2 = 4, a3 = 6, a4 = 8, a5 = 10
AHORA ES TU TURNO
Completa la siguiente tabla con los primeros diez términos de la sucesión que tiene como forma general:
an = 3n – 1
|
a1 = |
|
|
a2 = |
|
|
a3 = |
|
|
a4 = |
|
|
a5 = |
|
|
a6= |
|
|
a7 = |
|
|
a8 = |
|
|
a9 = |
|
|
a10 = |
ALGUNAS SUCESIONES DE IMPORTANCIA
El mundo de las sucesiones es muy diverso, al igual que sus diferentes tipos. Es por ello que a continuación se muestran las sucesiones más comunes:
• PROGRESIONES ARITMÉTICAS
Se conoce como progresión aritmética a la sucesión en la que cada término (a excepción del primero) resulta de sumar al anterior una cantidad fija denominada diferencia de la progresión y se denota con la letra d.
Cuando d>0 se trata de una progresión creciente porque los valores son cada vez mayores.
Cuando d<0 es una progresión decreciente, con valores cada vez menores.
Para determinar la diferencia de una progresión se deben restar dos términos consecutivos:
a2 –a1 = a3 –a2 = a4 –a3= …= an –an-1 = d
Observa estos dos tipos de progresiones aritméticas:
5, 8, 11, 14,… En este caso d = 3, por lo tanto se trata de una progresión creciente (d>0).
11, 9, 7, 5, 3,… Esta progresión cumplen que d = – 2, es decir, es una progresión decreciente (d<0).
Término General
Como en las progresiones aritméticas se cumple que cada término (menos el primero) resulta al sumar el término que le precede más la diferencia, se puede observar el siguiente comportamiento:
a2 = a1 + d
a3 = a2 + d = a1 + 2d
a4 = a3 + d = a1 + 3d
a5 = a4 + d = a1 + 4d
a6 = a5 + d = a1 + 5d
…
Siguiendo este comportamiento de manera sucesiva se puede expresar como término general para las progresiones aritméticas:
an=a1+ (n-1)d
Donde a1 es el primer término de la sucesión y d es la diferencia entre dos términos sucesivos.
APLICACIÓN DE LAS SUCESIONES
Debido a lo práctico que resulta expresar en forma general una secuencia ordenada de números, las sucesiones matemáticas han sido aplicadas en muchas disciplinas además de la matemática. Por ejemplo, las sucesiones de Fibonacci pueden ser aplicadas en el arte, en la informática y en la naturaleza.
Las progresiones son un tipo de sucesiones que se utilizan para realizar diversos cálculos como la determinación del interés compuesto. Otro uso de las progresiones aritméticas es en las interpolaciones (que consiste en calcular valores que se encuentran entre dos dados).
Por ejemplo:
Supongamos que se desean intercalar tres números entre 3 y 15 que llamaremos a, b y c de forma tal que se encuentren en progresión aritmética.
Se formaría la sucesión: 3, a, b, c, 15
Donde:
a1 = 3
a2 = a
a3 = b
a4 = c
a5 = 15
Recordemos que según la explicación de progresiones aritméticas a5 = a1 + 4d, de manera que si sustituimos a1 y a5 en la ecuación se puede determinar la diferencia de la progresión que es d:
a5 = a1 + 4d
15 = 3 + 4d → 12 = 4d → d = 3 (es una progresión creciente porque d>0).
Al conocer la diferencia se pueden calcular los demás valores ya que los miembros de una progresión aritmética (a diferencia del primer término) son el resultado de sumar la diferencia al término que le precede, es decir:
a1 = 3
a2 = a1 + d → 3 + 3 = 6
a3 = a2 + d → 6 + 3 = 9
a4 = a3 + d → 9 + 3 = 12
a5 = a4 + d → 12 + 3 = 15 (Aunque ya se conocía el valor del término a5 con anterioridad, al aplicar la definición de progresión aritmética se pudo comprobar nuevamente que era igual a 15).
De esta manera, al realizar la interpolación tenemos que los números que se encuentran entre 3 y 15 y forman una progresión aritmética son: 6, 9 y 12.

Los bancos emplean el cálculo del interés compuesto en los créditos que otorgan y para determinarlo utilizan cálculos de sucesiones matemáticas.
• PROGRESIONES GEOMÉTRICAS
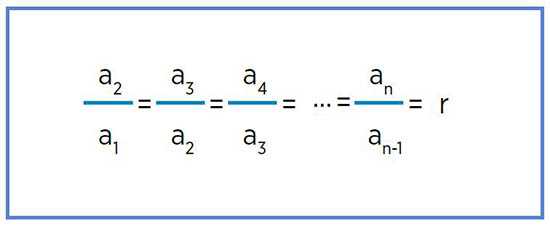
Son otro tipo de sucesiones donde cada término (exceptuando el primero) se calcula multiplicando al número anterior por una cantidad fija denominada razón de la progresión.
La razón se calcula al dividir dos términos consecutivos:
Término general
En este tipo de progresiones cada término es igual al producto de la razón y el término anterior:
a2 = a1.r
a3 = a2.r = a1.r2
a4 = a3.r = a1.r3
a5 = a4.r = a1.r4
…
Siguiendo este comportamiento de manera sucesiva se tiene como término general para una progresión geométrica:
an=a1.rn-1
• SUCESIONES DE POTENCIAS
En las sucesiones de potencias todos los términos cumplen con la característica de encontrarse elevados a un exponente.
Término General
Debido a que cada término de la sucesión se encuentra elevado a un mismo exponente. Este tipo de sucesión obedece a la siguiente forma:
1, 2m, 3m, 4m, 5m, 6m, …, nm,…
Donde m representa al exponente al cual se encuentran elevados todos los términos de la sucesión y pertenece a los números naturales.
• SUCESIONES DE FIBONACCI
Este tipo de sucesión lleva su nombre en honor al matemático italiano Leonardo Fibonacci y se caracteriza por el hecho de que cada número resulta de sumar los dos números anteriores a este. La forma más básica de este tipo de sucesión es:
1,1,2,3,5,8,13,21,34,55,89,144,233…
Término General
Las sucesiones de Fibonacci responden a esta forma:
an=an-1+an-2

A pesar de que Leonardo Fibonacci o Leonardo de Pisa diera a conocer las sucesiones que más adelante llevarían su nombre, ya éstas se encontraban descritas mucho antes en las matemáticas de la India.