Plano Cartesiano

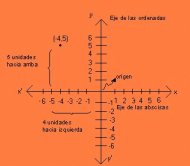
El plano cartesiano está formado por dos rectas numéricas perpendiculares entre sí, siendo una de éstas una recta horizontal y otra vertical, las cuales se cortan en un punto.

La recta horizontal es llamada “eje de las abscisas” o “eje de las X”, y la recta vertical es llamada “eje de las ordenadas” o “eje de las Y”; el punto donde se cortan ambas rectas perpendiculares recibe el nombre de origen, siendo el punto (0,0).

El plano cartesiano es una representación gráfica de referencia, éste tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados.

Las coordenadas cartesianas, también llamadas coordenadas rectangulares, son un claro ejemplo de coordenadas ortogonales, y éstas se forman asociando un valor del eje de las abscisas con un valor del eje de las ordenadas, respectivamente, esto indica que un punto, que en general se representa con una letra mayúscula, por ejemplo: (P), éste se puede ubicar en el plano cartesiano tomando como base sus coordenadas, y se representa de la siguiente manera:

P (x, y)

Las dos rectas al cortarse, dividen al plano en cuatro regiones, estas zonas se conocen como “cuadrantes” y se ordenan así:

• Primer cuadrante "I”: está ubicado en la región superior derecha.
• Segundo cuadrante "II": está ubicado en la región superior izquierda.
• Tercer cuadrante "III": se encuentra ubicado en la región inferior izquierda.
• Cuarto cuadrante "IV": este se encuentra ubicado en la región inferior derecha.

El plano cartesiano se utiliza para asignarle una ubicación a cualquier punto en el plano.

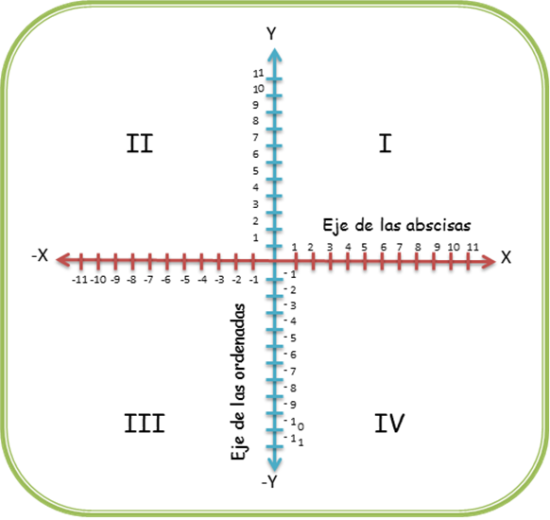
Localizar un punto en el plano cartesiano.

Para ubicar un punto cualquiera o un par ordenado en el plano cartesiano, se siguen los siguientes pasos:

1. Para localizar el valor de la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas, o hacia la izquierda si son negativas, a partir del punto de origen, donde éste es cero.

2. Para localizar el valor del eje de las ordenadas, desde donde se localizó el valor de x, se cuentan las unidades correspondientes, hacia arriba si son positivas o hacia abajo, si son negativas.

3. Por último se coloca un punto (.), de pequeña dimensión, señalando de esta forma la localización del punto dadas ambas coordenadas.

Por ejemplo, localizar los puntos:

A (5,-3), B (2,6) , C (-9,-6)