VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS


Un número es un concepto que expresa una cantidad en relación a su unidad. También puede indicar el orden de una serie o, en sentido amplio, indicar el carácter gráfico que sirve para representarlo, cuyo signo recibe el nombre de numeral o cifra. Por lo demás, aquel que se escribe solo con un guarismo se llama dígito.
En matemática moderna, el concepto de número incluye tantas abstracciones que fue necesario que se estudiaran sus propiedades a través de una teoría de los números para que pudieran ser clasificados.
Desde la época de Euclides, matemático y geómetra griego cuya vida se cree transcurrió en Alejandría durante el reinado de Ptolomeo I, hasta Carl Friedrich Gauss, matemático, astrónomo, y físico alemán nacido en 1777, el avance en el conocimiento de los números fue espectacular, y aunque hasta el día de hoy pueden faltar muchas cosas por descubrir, éstas serán siempre sobre la base de la obra de ambos.
Alrededor del año 300 a. C., Euclides recogió todo el saber disponible en ese momento en la referente a matemática antigua y lo plasmó en trece libros a los que denominó Elementos, obra que con el devenir de los siglos ha sido fuente de consulta de numerosos investigadores.
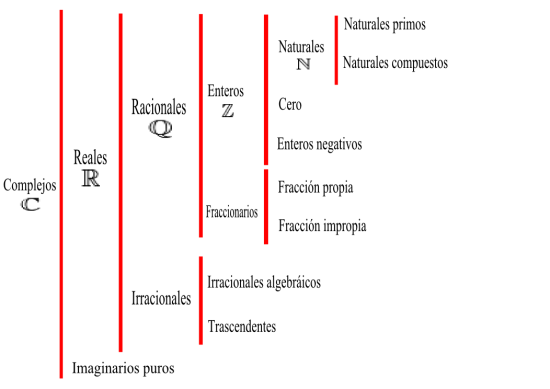
Hacia el 1800, Gauss llevó a cabo algo similar con su obra Disquisitiones Arithmeticae, que recogió todo el saber que hasta entonces se tenía de la teoría de los números y que no pasaba de ser una mera colección de resultados aislados. Fue entonces, en su “Magnum Opus”, que Gauss introdujo la noción de congruencia y, al hacerlo, unificó la teoría de los números. Allí, para Gauss, los números se pueden clasificar de la siguiente manera:
Son aquellos números que se utilizan para contar. Se llaman “naturales” porque fueron los primeros que usó el ser humano para contar.
Debido a que los números naturales se utilizan para contar objetos, el cero puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del autor y la tradición, el conjunto de los números naturales puede presentarse entonces de dos maneras distintas:
ℵ={1,2,3,4,...}
ℵ0={0,1,2,3,4,...}
Este conjunto de números, pues, se caracteriza por:
A estos números se los representa con la letra Z. En este grupo se incluyen a los números naturales distintos de cero (1, 2, 3,...), los negativos de los números naturales (..., -3, -2, -1) y al cero mismo. Su definición, entonces, es la siguiente:
Z ={..., -2, -1, 0, +1, +2,...}
El orden de los números enteros puede definirse como:
La palabra racional se deriva de “razón”, por ello, los números racionales son aquellos que se obtienen mediante la razón (división) de dos números enteros. Por lo tanto, un número racional puede representarse como el cociente de dos números enteros; esto es, una fracción común a/b con numerador a y denominador b distinto de cero. El conjunto de números racionales se representa por Q , inicial de quotient, que significa “cociente” en inglés. Este conjunto de números incluye a los números enteros (Z), y es un subconjunto de los números reales (ℜ ).
Se llaman números irracionales a los que no tienen una forma decimal periódica y, por lo tanto, no pueden expresarse en forma de fracción. Aunque no existe una notación universal para indicarlos, generalmente se acepta su representación por Π.
Se llaman así al conjunto formado por los números racionales e irracionales y se representan con la letra ℜ. Por definición, entonces, tenemos que ℜ es la unión de los conjuntos Q e Π .
Con números reales pueden realizarse todo tipo de operaciones básicas, salvo en dos excepciones importantes:
Los números complejos describen la suma de un número real y un número imaginario. Por lo general, los números complejos se utilizan en todos los campos de las matemáticas, en muchos de la física y en ingeniería, especialmente en la electrónica y las telecomunicaciones por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica. Con todo, son una extensión de los números reales, cumpliéndose que ℜ ⊂ C.
De esta manera, al contener a los números reales y los imaginarios puros, constituyen una de las construcciones teóricas más importantes de la inteligencia humana.