Ecuaciones en Q

Las fracciones aparecen al dividir un todo o unidad en partes iguales y tomar varias de esas partes. Por ejemplo, si una torta se divide en 12 partes iguales y Juan se come 5 partes ¿Que porción queda de la torta? Quedarían 7/12.

Para resolver ecuaciones con coeficientes racionales o fracciones se sigue el mismo procedimiento que se aplica para resolver las ecuaciones de números enteros o Z.

Se pueden seguir los siguientes pasos para resolver el siguiente problema:

a) Se eliminan los denominadores, para ello se multiplica cada uno de los términos de la ecuación por el mínimo común múltiplo de los denominadores. En este caso m.c.m (2,5) = 10

b) Se reducen los términos semejantes, es decir, se suman o se restan los términos que contienen a x en cada miembro, así como los términos constantes.

-3x + 60 = 10x + 120

c) Se agrupan los términos que contienen a x en el primer miembro y los términos constantes en el segundo

-3x - 10x = -60 + 120

d) Se reducen los términos entre sí:

-13x = 60

e) Por último se despeja la x; para ello se dividen cada uno de los términos entre -13:

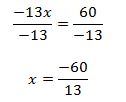
Para verificar la solución se sustituye el valor de x en la ecuación inicial.

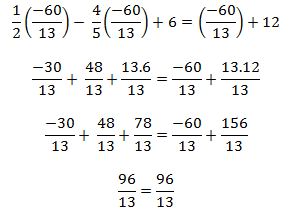
Como ambos miembros son iguales, entonces

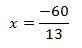
Siendo x la solución de la ecuación.

Cada uno de los pasos realizados en el ejemplo de ecuación en Q anteriormente descritos, convierten la ecuación en una equivalente a ella pero más sencilla, y dos ecuaciones son equivalentes si tienen las mismas soluciones.

De esta misma manera, se pueden presentar situaciones problemáticas, y su solución la podemos encontrar aplicando nuestros conocimientos de ecuaciones en Q, para ello debemos seguir 4 pasos muy sencillos:

a). Comprensión del problema.

b). Planteamiento de la ecuación.

c). Resolución de la ecuación.

d). Verificación de la solución.

Por ejemplo:

Un equipo de béisbol ha ganado 13 juegos y ha perdido 9. ¿Cuántos juegos tiene que ganar consecutivamente para tener 2/3 de juegos ganados?

a). Sea x el número de juegos que necesita ganar consecutivamente el equipo.

b). La cantidad de juegos que ganara en total es 13 + x, este número debe ser igual a los 2/3 de los jugados en total.

Los juegos jugados en total deben ser iguales al total de juegos ganados, más los juegos perdidos:

La ecuación es:

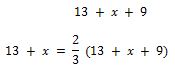
c) Solución de la ecuación:

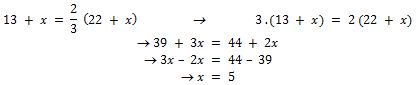
El equipo debe ganar 5 juegos seguidos.

d) El total de Juegos ganados debe ser:

13 + 5 = 18

y los juegos jugados,

18 + 9 = 27

La condición indica que el total de juegos ganados deber ser 2/3 de los jugados, verificando el valor de la x conseguido: