Entalpía

Para un cambio de estado a presión constante la formulación de la primera ley de la termodinámica se convierte en:

dU = dQ_p - pdV

Donde U es la energía interna, Q_p es el calor, p la presión y V el volumen. Dado que p es constante, de la integración resulta:

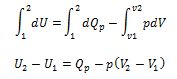
Reordenando, se obtiene:

(U₂ + pV₂) - (U₁ + pV₁) = Q_p

La función U + pV, que es un combinación de variables de estado, es en sí misma una variable de estado, H. Definimos

H ≡ U + pV

H, se denomina entalpía del sistema, una propiedad extensiva de estado. Utilizando la definición de H puede expresarse la ecuación como H₂ - H₂ = Q_p o bien:

ΔH = Q_p

Para un cambio infinitesimal en el estado de un sistema, la ecuación anterior toma la forma;

dH = dQ_p

Como H es una función de estado, dH es una diferencial exacta. Escogiendo T y p como variables convenientes de H, la diferencial total puede expresarse como:

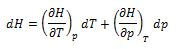
Para una trasformación a presión constante, es decir: dp = 0, la ecuación anterior, se convierte en dH = (∂H/∂T)pdT. Combinando esta expresión con la ecuación (7), se obtiene:

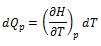
Que relaciona el calor transferido desde el entorno con el aumento de la temperatura del sistema. La razón dQ_p/dT = C_p, la capacidad calorífica del sistema a presión constante. Por consiguiente se tiene:

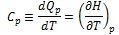
Que identifica la importante derivada parcial (∂H/∂T)_p con la cantidad medible C_p. En lo sucesivo, la diferencial total en la ecuación (10), se expresará de la forma:

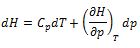
Para cualquier transformación a presión constante, como dp = 0, la ecuacion siguiente se reduce a:

dH = C_pdT

O, para un cambio finito de estado de T₁ a T₂:

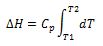
Si C_p es constante en el intervalo de temperatura que nos interesa, la ecuación anterior, se convierte en:

ΔH = C_pΔT