Función numérica

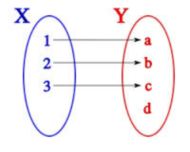
Una función numérica es una relación cuyo dominio y codominio son conjuntos de números, es decir si A y B son conjuntos de números y están relacionados, entonces:

ƒ: A → B

La función ƒ del conjunto A en el conjunto B estará determinada por una proposición, la cual debe indicarnos cómo se construyen las imágenes, es decir, por una fórmula que indique la imagen de cada elemento del dominio.

En otras palabras, si se tienen dos conjuntos A y B, una función (relación) entre estos conjuntos es una asociación ƒ que a cada elemento de A le asigna un único elemento de B, siendo A el dominio de ƒ y B el codominio.

Si tenemos una función tal que &fnof: A→B, y esta asocia a cada número su cuadrado, así:

ƒ(0) = 0² = 0

ƒ(1) = 1² = 1

ƒ(2) = 2² = 4

ƒ(3) = 3² = 9

ƒ(4) = 4² = 16

Por lo observado, podemos construir una fórmula que reproduzca cada resultado (imagen) de esa función, así:

ƒ(x) = x²

También podemos encontrar una función expresada así:

y = ƒ(x)

Esta expresión nos enuncia que “y” es la imagen del elemento “x” del dominio de la función f. De acá podemos observar los elementos característicos de una función, la letra “x” se llama variable independiente, mientras que la letra “y” se llama variable dependiente.

La letra “x” esta puede ser cambiada por cualquier otra letra sin afectar en lo absoluto a la función, por ejemplo:

y = ƒ(x) = 2x + 5

También puede ser escrita así:

y = ƒ(x) = 2t + 5

Ahora observa el siguiente diagrama sagital:

También puede presentarse el caso en el que nos den un enunciado tal que los datos brindados en él nos permitan construir una función, por ejemplo:

Expresar mediante una fórmula la función ƒ:A → B, que asigne a cada número real su quinta parte, y de aquí hallar ƒ(3) y ƒ(10/3)

La función puede ser expresada así:

y = ƒ(x) = x/5

Para determinar ƒ(3) y ƒ(10/3), debemos sustituir los valores entre paréntesis, que son los valores que tendrá x, en la función.

ƒ(x) = x/5 → ƒ(x) = 3/5

ƒ(x) = (10/3)/5 = 10.(1)/3.(5) = 10/15 = 2/3

También es posible que en una proposición nos den la función, de tal modo que de esta fórmula se pueda obtener la imagen de cada elemento del dominio.

Ejemplo:

Dada la función p:Z → Z, que se encuentra definida así:

p(x) = 3x + 6

Encontrar los valores correspondientes a: p(2), p(-2), p(0) y p(10)

Para solucionar este tipo de planteamiento procedemos de la siguiente manera:

p(2) = 3.(2) + 6 = 12

p(-2) = 3(-2) + 6 = 0

p(0) = 3.0 + 6 = 6

p(10) = 3.(10) + 6= 36

De acuerdo a lo observado en los ejemplos anteriores, cuando una función está dada por una fórmula y se quiere conocer la imagen de cualquier elemento del dominio, solo se debe sustituir la variable independiente por dicho elemento del dominio, y luego realizar las operaciones pertinentes.

Ejemplo:

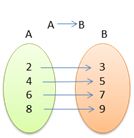
Dado el conjunto A = {2,4,6,8}, y la función: ƒ(x) = x + 1, determinar el conjunto B para que se cumpla ƒ:A → B. Halla el dominio y el rango de la función. Hacer el diagrama sagital correspondiente.

Para hallar el conjunto B, sustituimos cada valor del conjunto A en la función dada.

ƒ(2) = 2 + 1 = 3

ƒ(4) = 4 + 1 = 5

ƒ(6) = 6 + 1 = 7

ƒ(8) = 8 + 1 = 9

Conjunto B = {3,5,7,9}

Dom ƒ = {2,4,6,8}

Rg v = {3,5,7,9}