 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS

La palabra función proviene del latin function, que significa cumplimiento, ejecución. De esta conceptualización podemos afirmar que una función es una correspondencia, pero entre conjuntos, uno de partida y uno de llegada, de aquí que una función es una relación, pero para que una relación pueda ser llamada así, función, debe cumplir ciertas condiciones.
Una función ƒ será una relación si se cumplen las siguientes condiciones:
Si ƒ es una función del conjunto A en el conjunto B, esto matemáticamente o en lenguaje matemático puede ser expresado así:
ƒ: A → B
El conjunto formado por los elementos del conjunto de partida recibe el nombre de: Dominio, y se denota: Dom ƒ; del mismo modo cada uno de los elementos del conjunto de llegada que están relacionados reciben su nombre: Imágenes. El conjunto formado solo por aquellos elementos del codominio que son imágenes recibe el nombre de Rango, y se denota: Rg ƒ, siendo este un subconjunto del codominio.
De manera que una función de A en B es una correspondencia que asigna a cada elemento de A una única imagen de B, así mismo una función es una relación y por tanto se puede describir mediante un diagrama sagital o en pares ordenados.
Observemos el siguiente ejemplo:

ƒ: A→? B = {(1,2),(2,4),(3,6),(4,8),(5,10)}
Dom F = {1,2,3,4,5}
Rg ƒ = (2,4,6,8,10)
No todas las relaciones son funciones, recordemos se deben cumplir las dos condiciones anteriormente expuestas, observemos el siguiente ejemplo:


Esta relación sí es una función, porque todos los elementos del conjunto de partida están relacionados y cada uno de ellos tiene una sola imagen.
Dom ƒ = {1,2,3,4}
Rg ƒ = {A,B,C}
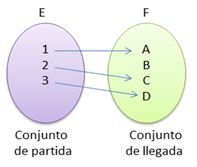
Esta relación es una función, esto se debe a que todos los elementos del conjunto de partida están relacionados y cada uno de ellos solo tiene una imagen.
Dom ƒ = {1,2,3}
Rg ƒ = {A,C,D}
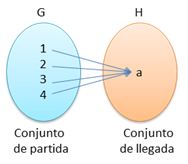
Sí es una función esta relación, por la condición que nos dice, que en una función todos los elementos del conjunto de partida deben estar relacionados, además de poseer una sola imagen. En este caso en particular, el conjunto de llegada y el rango coinciden, asimismo todos los elementos del dominio tienen la misma imagen.
Dom ƒ = {1,2,3,4}
Rg ƒ = {a}
También puede ocurrir que el conjunto de partida esté formado por un solo elemento, al mismo tiempo que el conjunto de llegada también contenga un solo elemento, y estos estar relacionados, en este caso esta relación también será una función, donde el codominio y el rango coinciden.

Dom ƒ = {1}
Rg ƒ = {a}