Mínimo común múltiplo y Máximo común divisor

Ya hemos estudiado el m. c. m. y el m. c. d., por lo tanto sabemos obtener esos valores de un solo número o de varios números de manera simultánea. En esta oportunidad aplicaremos estos conocimientos para resolver algunos problemas.

En la vida diaria se pueden presentar casos o problemas en donde el uso del m. c. m. y el m. c. d., nos ayuda a encontrar la solución.

A continuación presentaremos varios ejercicios propuestos para que los estudiantes se guíen en el empleo, uso, y desarrollo de problemas relacionados con m. c. m. y m. c. d.

Problema 1

Un viajero va a Buenos Aires cada 18 días y otro cada 24 días. Hoy han estado los dos en Buenos Aires.

¿Dentro de cuantos días volverán a estar los dos a la vez en Buenos Aires?

Si resolvemos este mismo ejercicio realizando el m. c. m. simultáneamente, es decir, resolviendo el mínimo de ambos números al mismo tiempo, obtenemos:

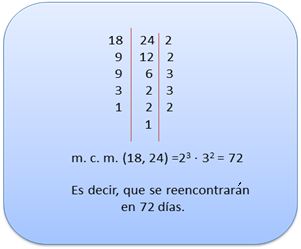
Problema 2

Un Semáforo se enciende cada 12 segundos, otro cada 18 segundos y un tercero cada 1 minuto. A las 8:00 de la mañana los tres semáforos coinciden. ¿Cuántas veces volverán a coincidir en los próximos 10 minutos?

Para resolver este problema es necesario obtener el mínimo común múltiplo de las tres cifras:

Para conocer cuántas veces coincidirán en los próximos diez minutos, es necesario realizar una división, 10 minutos son equivalentes a 600 segundos, al dividir, 600s/180s = 3.33, lo que significa coincidirán solo 3 veces a las 8:03, 8:06 y 8:09.

Problema 3

Un comerciante desea poner en cajas 12.028 manzanas y 12.772 naranjas, repartiéndolas de modo que cada una de las cajas contenga el mismo número de manzanas o de naranjas y, además, el mayor número posible de ellas. Hallar el número de naranjas de cada caja y el número de cajas necesarias.

Para responder calculamos el máximo común divisor de cada una de las cantidades de frutas.

Para saber la cantidad de cajas necesarias dividimos el número total de frutas entre la cantidad de frutas que llevará cada caja; que ya lo calculamos y serán 124 frutas, bien sean manzanas o naranjas.

Cajas de naranjas = 12.772 / 124 = 103.

Cajas de manzanas = 12.028 / 124 = 97.

Cajas necesarias = 103 + 97 = 200.

Problema 4

Un cuarto tiene las siguientes medidas: 12 metros de longitud y 6,8 metros de anchura. Calcula cuánto debe medir la mayor baldosa cuadrada que cabe un número exacto de veces en esa habitación; además, expresa cuántas baldosas se necesitan para embaldosar todo el cuarto.

Lo primero que debemos hacer es realizar la conversión pertinente de metros a centímetros así:

12 metros = 1200 cm.

6,8 metros = 680 cm.

Ahora, debemos obtener el m. c. d de ambas cifras:

Sabiendo que cada baldosa debe medir 40 centímetros de lado, debemos calcular el área que ocupará cada una de ellas:

Área_baldosas: (40cm)² = 1.600cm²

A_cuarto: 1.200cm x 680 cm = 816.000 cm²

Conociendo el área total de la habitación, podemos calcular el número de baldosas que se necesitan, de la siguiente manera:

816.000 ÷ 1.600 = 510 Baldosas.