 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS


Multiplicar y dividir fracciones es muy sencillo. Comencemos primero por una multiplicación.
Multiplicación
4 2
— . — =
5 3
Para multiplicar dos fracciones se realiza la multiplicación de los numeradores y la multiplicación de los denominadores, de la siguiente forma:
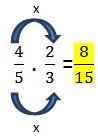
Se debe simplificar el resultado si es necesario, en este caso, la fracción ya es irreducible.
Cuando es posible, se pueden realizar simplificaciones antes de realizar la multiplicación, veamos otro ejemplo:
4 10
— . — =
25 12
En esta multiplicación podemos observar que hay números que tienen divisores comunes.
Veamos los divisores de cada número:
4 = {4,2,1}
10 = {10,5,2,1}
12 = {12,6,4,3,2,1}
25 = {25,5,1}
Podemos observar que 10 y 25 tienen como divisor común al 5 (el 1 no debemos tenerlo en cuenta, ya que no nos sirve para simplificar).
El 4, 10 y 12 tienen como divisor común al 2.
Ya estamos en condiciones de comenzar a simplificar:
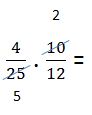
Siempre se simplifica un numerador con un denominador. Es decir: Se simplifica un número de “arriba” con uno de “abajo”. Dividiendo a ambos por un mismo número, en este caso fue por 5.
Luego de la primera simplificación nos queda:
4 2
— . — =
5 12
Entonces debemos continuar simplificando:
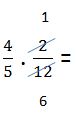
En este caso simplificamos, dividiendo por 2.
Se puede simplificar sobre la misma fracción o en forma cruzada, como en el paso anterior.
Aún nos queda una simplificación, ya que 4 y 6 son divisibles por 2.
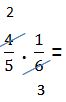
2 1
— . —
5 3
Cuando ya no tenemos más posibilidad de simplificar, realizamos la multiplicación:
2 1 2
— . — = —
5 3 15
“Para multiplicar tres o más fracciones se sigue el mismo procedimiento: simplificar, multiplicar todos los numeradores para obtener el numerador producto. Del mismo modo con los denominadores.”
División
3 1
— : — =
5 2
Para realizar la división tenemos dos posibilidades:
3 1 3 2
— : — = — . —
5 2 5 1
Luego multiplicar como ya vimos:
3 2 6
— . — = —
5 1 5
Otra forma es multiplicar en forma cruzada, de este modo:
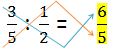
Al igual que con las multiplicaciones se debe revisar si la respuesta final es una fracción irreducible. Si no lo es, se procede a simplificar.
Ejercitación
3 2
a). — . — =
7 5
16 2
b). — . — =
5 4
7 2
c). — : — =
5 9
3 9
d). — : — =
5 15
9 2 5
e). — . — . — =
5 6 8