VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
A diario se presentan situaciones en donde debemos relacionar o asociar elementos de un conjunto con elementos de otros conjuntos, e incluso con elementos del mismo conjunto.
Un conjunto es una colección de objetos no repetidos, estos objetos reciben el nombre de elementos; si x es un elemento de un conjunto A, esto se representa así:

Siendo todas las expresiones equivalentes.
Cuando un elemento no pertenece a un conjunto, por ejemplo, si x no pertenece al conjunto A, se expresa así:
x ∉ A
Además, puede ocurrir que un conjunto sea parte de otro mayor, a éste se le llama subconjunto, es decir, un subconjunto es la parte de un conjunto. Por ejemplo:
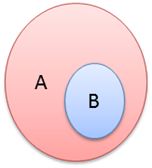
En este caso se dice que B es un subconjunto de A, pues está contenido en A. Así mismo se puede expresar en lenguaje matemático, así:
B ⊂ A
Cuando se tienen dos conjuntos, estos se pueden encontrar relacionados, por ejemplo:
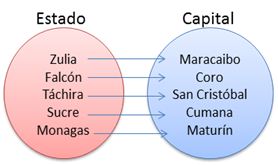
De esta forma, se puede observar que los conjuntos “Estados y Capitales” están relacionados, y la manera de representar esta asociación es con el diagrama anteriormente expuesto.
También es posible organizar esta asociación en forma de par ordenado, es decir, (Zulia, Maracaibo), (Falcón, Coro), (Táchira, San Cristóbal), (Sucre, Cumana), (Monagas, Maturín).
Un par es un conjunto que está formado por dos elementos; el orden, implica la colocación de elementos en los lugares que le corresponden; una relación es una conexión, una correspondencia entre una cosa y otra.
Un par ordenado es un conjunto formado por dos elementos colocados en un orden, éste se representa colocando los dos elementos entre paréntesis y separados por una coma.
Si se tiene el par ordenado: (a,b), éste tendrá los elemento a y b en ese orden; si ahora se tiene el par ordenado: (b,a), este par será distinto al anterior, es decir, los pares ordenados (a,b) y (b,a) son distintos a pesar de tener los mismos elementos, esto se debe a que tienen un orden distinto.
En un par ordenado los elementos se llaman componentes o coordenadas, por ejemplo, en el par ordenado (1,2) el elemento “1” es el primer componente del par ordenado (1,2) y “2” es el segundo componente o segunda coordenada de tal par ordenado.
Para dos conjuntos que se encuentran relacionados, conjunto A y conjunto B, al conjunto A se le llama conjunto de partida y al conjunto B se le llama conjunto de llegada o codominio.
Una relación entre dos conjuntos puede ser representada y visualizada escribiendo sus pares ordenados o realizando un diagrama sagital, de la siguiente manera:
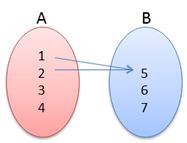
En este diagrama sagital los pares ordenados se establecen mediante flechas dirigidas, que van desde la primera componente hasta la segunda; para este diagrama la relación R= {(1,5), (2,5)}.
De forma general, una relación es un conjunto de pares ordenados; de los conjuntos anteriores A y B, ellos se encuentran relacionados: R = {(1,5), (2,5)}, es una relación del conjunto A={1,2,3,4} en el conjunto B={5,6,7}, ya que las primeras componentes de los pares ordenados están en A y sus segundas componentes o coordenadas están en B, de aquí se tiene que:
(1,5) ∈ R y (2,3) ∉ R
Una relación puede expresarse mediante una proposición, por ejemplo:
Una posible solución para el planteamiento anterior es:
A={1,2,3,4,5}
B={3,6,9,12,15}
R = es el triple de
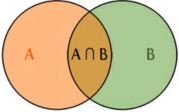
Pares ordenados: R= {(1,3), (2,6), (3,9), (4,12), (5,15)}
Esta relación de pares ordenados puede ser representada en el siguiente diagrama sagital: