Teorema de Thales

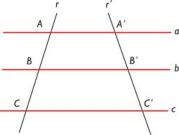
Definición: Si tres o más paralelas son cortadas por dos transversales, la razón de las medidas de los segmentos determinados en una de las transversales es igual a la razón de las medidas de los segmentos correspondientes determinados en la otra.

__    __                                                                      __    __     __    __
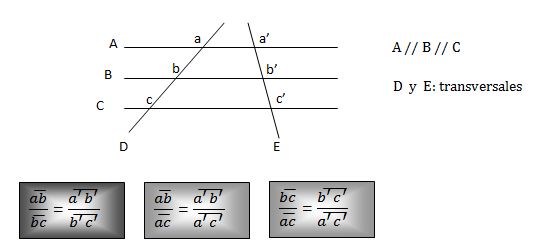
ab y a'b' son segmentos correspondientes, al igual que bc y b’c’, ac y a’c’. Se pueden utilizar las razones vistas o sus inversas. Por ejemplo:

Veamos cómo realizar ejercicios utilizando el Teorema de Thales.

Ejercicio 1:

                                                __
Calcular la medida del segmento b'c'

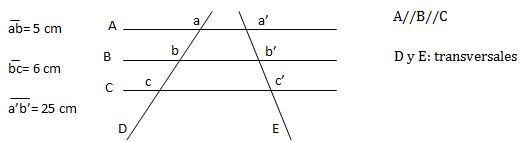
Luego de ver los datos que nos ofrece el ejercicio, elegimos qué razones utilizar.

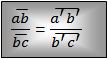
Procedemos luego a reemplazar los datos en la ecuación:

                                      __
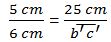
Despejamos el segmento b'c':

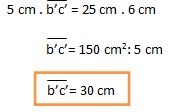
Ejercicio 2:

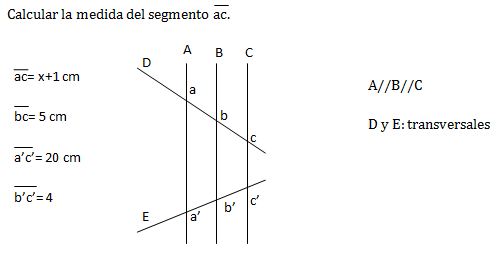
De acuerdo a los segmentos dados, debemos relacionarlos así:

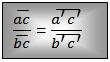
Luego reemplazamos con los datos dados:

x+1   20
— =   —
5         4

Resolvemos:

(x + 1).4 = 20.5

x + 1 = 100:4

x + 1 = 25

x = 25 - 1

x = 24 cm Debemos recordar colocar la unidad al finalizar.

                                                           __
Cómo se solicitaba calcular el segmento ac, aún nos queda un paso por realizar:

__
ac = x + 1 cm

__
ac = 24 cm + 1 cm = 25 cm

__
ac = 25 cm

Comprobamos

25cm   20cm
  —     .   —     =
5cm      4cm

25    20
—  .  — =
 5       4

5 = 5