VOLVER A LOS ARTÍCULOS
Si se coloca un imán en el interior de un campo magnético, tiende a orientarse por sí mismo, de tal manera que el polo norte señale en la dirección y sentido del campo magnético B.
Existe una fuerza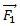 
que actúa sobre el polo norte con dirección y sentido de 
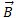y otra 
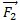, de igual magnitud pero sentido opuesto, actuando sobre el polo sur. La intensidad del polo del imán se calcula con el cociente entre la fuerza que se ejerce sobre el polo y el valor del campo magnético:
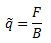
Si se opta por la convención de signos de que el polo norte es + y el sur es -, la fuerza puede escribirse:
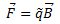
Se puede ver que existe un momento (también llamado torque) de la fuerza que actúa sobre el imán dentro del campo magnético.
Si llamamos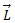 
al vector que señala del polo sur al polo norte, con el valor de la distancia entre ellos, el momento es:
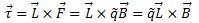
Se define el momento magnético como: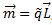 
, entonces:
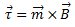
Esta expresión también puede escribirse de la siguiente manera:
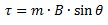
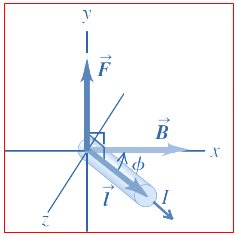
Cuando se tiene un conductor por el cual circula una corriente se lo introduce en un campo magnético , siente una fuerza 
producto de ese campo que interacciona con la corriente que circula en él.
Siendo I, la corriente que circula por el conductor, 
la longitud del conductor, tenemos que la fuerza se expresa de la siguiente manera:
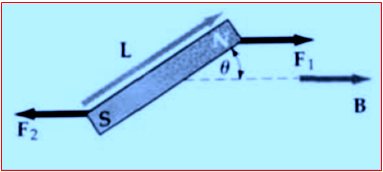
F = I . l . B . sin θ
Siendo θ el ángulo comprendido entre el campo eléctrico y el conductor.
Para el caso que se tiene una espira de largo a y ancho b por la cual circula una corriente, y está dentro de un campo magnético se puede calcular las fuerzas y el torque de ellas debido al campo magnético.
F1 = F2 = IaB
Dado que el área de la espira es: A = a . b el torque es:
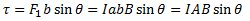
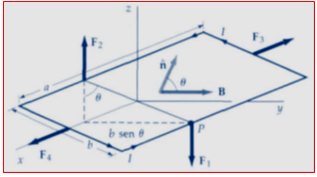
Para una espira de N vueltas:
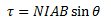
El momento dipolar magnético es:
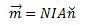
Entonces el torque se expresa:
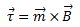
O bien:
