Inecuaciones

Trabajar con inecuaciones es similar a trabajar con ecuaciones. Las reglas que hay que seguir para resolver una ecuación también se aplican a las inecuaciones, solo que, en este último caso, se agregan algunas más.

Comencemos repasando algunos símbolos que vamos a utilizar.

El símbolo < “menor que” se utiliza para indicar el orden de los números. En la recta numérica, siempre vamos a encontrar un número que es mayor que otro y viceversa.

Al escribir a<b estamos diciendo que el número “a” es menor que “b” dicho de otro modo, si tenemos que ubicar estos números en la recta numérica, veremos que el número “a” se encuentra a la izquierda del número “b”.

También podemos deducir de esto último que si restamos ambos números (b-a), obtendremos como resultado un número positivo.

Al símbolo > “mayor que” lo utilizamos para indicar, entre dos números, cuál es mayor. La expresión “b>a” se lee b es mayor que a y esto significa que la operación “b-a” da como resultado un número positivo.

En este caso, si ubicamos estos números en la recta numérica vamos a encontrar al número b a la derecha de a.

Reglas para resolver inecuaciones

1) Todo número que se encuentra sumando en un lado de la desigualdad, pasa al otro lado restando.

2) Todo número que se encuentra restando en un lado de la desigualdad, pasa al otro sumando.

3) Si en un lado de la desigualdad hay un número negativo multiplicando, pasa al otro lado dividiendo (con su signo) y el signo de desigualdad se debe invertir.

4) Si en un lado de la desigualdad hay un número negativo dividiendo, pasa al otro lado multiplicando (con su signo) y el signo de desigualdad se debe invertir.

Ejemplo

a) Resolver la siguiente desigualdad.

2X + 3 - 5/2X > 24 - X

2x+3 - 5/2x > 24 - x	Sumamos en el primer miembro los términos que tienen X.
- 1/2 x +3 > 24 – x	Agrupamos los términos que tienen X de un lado de la desigualdad, y los números del otro lado.
- 1/2 x +x > 24 – 3	Realizamos las operaciones.
1/2 x > 21	Pasamos dividiendo el 1/2 al miembro derecho de la inecuación.
x > 21: 1/2	Realizamos las cuentas.
X > 42	Resultado final.

a) Resolver la siguiente desigualdad.

-3X + 5 > 15 + 2X

-3X + 5 > 15 + 2X	Agrupamos los términos con X de un lado y los números del otro.
-3X - 2X > 15 - 5	Realizamos las operaciones.
-5X > 10	Pasamos al número negativo, que acompaña multiplicando a la X, dividiendo al otro lado. Como el número es negativo el signo de desigualdad se invierte.
X < 10 / (-5)	Resolvemos la operación.
X < -2	Resultado final.

Inecuaciones con valor absoluto

El valor absoluto de un número real x se escribe |x|

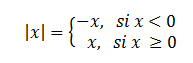
Es decir, el valor absoluto de un número negativo es igual al mismo número con signo positivo. El valor absoluto de los números positivos, incluido el cero, es igual al número dado.

Propiedades del valor absoluto

• |x|=|-x|
• |x.y|=|x|.|y|
• |x+y|=|x|+|y|

Recordar

Ejemplo

Resolver la siguiente inecuación.

2.|3X| - 6 > (|2X| + 3).2

2.|3X|- 6 > (|2X|+3).2	Aplicamos la propiedad distributiva a la derecha de la desigualdad.
6|X| - 6 > 4|X| + 6	Agrupamos de un lado los términos que tienen |x|, y del otro los números.
6|X| - 4|X | > 6 + 6	Realizamos las operaciones.
2|X| > 12	Pasamos el 2 dividiendo al otro lado. Como pasamos un número positivo la desigualdad no se invierte.
|X| > 12/2	Resolvemos la operación.
|X| > 6	Recordamos que |x| > a → -a > o a < x
X > 6 o X < -6	Respuesta final.