ECUACIONES EXPONENCIALES

En este tipo de ecuaciones la incógnita se encuentra en el exponente. Para resolverlas, es necesario recordar las propiedades de las potencias.

PROPIEDADES DE LAS POTENCIAS:

La mejor manera de aprender este tema es resolviendo algunos ejercicios, ya que se pueden utilizar diversas estrategias de resolución, dependiendo la ecuación exponencial con la que tengamos que trabajar:

^{1) 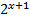 = 4}

En este ejercicio, observamos que hay un solo término a cada lado del igual. Uno de ellos tiene en su exponente la incógnita, con lo cual identificamos que nos encontramos ante una ecuación exponencial.

Una estrategia sencilla para resolverla es la siguiente:

=	Reemplazamos el 4 por su equivalente: . Esto lo hacemos para obtener bases iguales en cada miembro de la ecuación.

=

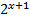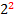
Las bases son las mismas, por lo tanto, para mantener la igualdad, los exponentes también deben ser iguales.

De allí, que:

x+1=2

A continuación solamente nos falta despejar la x para obtener la respuesta final.

x=2-1

x=1

---------------------------------------------

^{2) 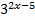 = 1}

En el lado derecho de la igualdad hay un 1, como sabemos que a^0 = 1 (propiedad), podemos decir lo siguiente:

= 1	Porque 3°=1

Por lo tanto

2x-5=0

2x=0+5

x=5/2

---------------------------------------------

^{3) 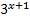 +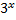= 324}

Para resolverlo utilizamos la siguiente propiedad:

^{. =}

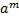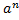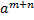
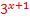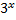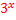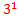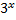^{+= 324}

^{.+= 324}

^{Luego resolvemos}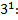

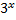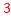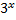^{.+= 324}

Ordenamos colocando el coeficiente 3 delante de 3^x:

3.3^x+3^x=324

Sumamos 3.3x+3x:

Debemos tener en cuenta que 3x=1.3x Por ello: 3.3x+1.3x=4.3x

4.3^x=324

Pasamos el 4 dividiendo:

3^x=324:4

3^x=81

3^x=3⁴

Al obtener bases iguales, los exponentes también son iguales. Por lo tanto:

x=4

---------------------------------------------

4)  2^xx - 7.2^x- 8 = 0

En primer lugar, se identifican los factores que contienen el exponente que contiene la incógnita (x).

Luego se reescribe la ecuación de la siguiente manera:

(2^x)²- 7 . 2^x- 8 = 0

Esto se realiza para poder hacer una sustitución, es este caso: y=2^x. Quedando:

y²- 7 y - 8 = 0

De este modo se logra obtener una ecuación que puede ser resuelta mediante la fórmula resolvente.

Y_1,2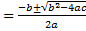

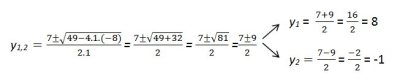
Y₁ = 8

Y₂ = -1

Una vez que obtenemos los posibles valores de y, reemplazamos:

y= 2 x 8= 2 x 23 = 2 x

No existe un número x que haga posible la igualdad. - 1 = 2 x

3 = x

x=3

De este modo hallamos el resultado de una ecuación exponencial de este tipo.