Ecuaciones logarítmicas

Antes de comenzar la resolución de algunos ejercicios con ecuaciones que contienen logaritmos, debes recordar las propiedades de los mismos y la definición de logaritmo.

PROPIEDADES DE LOS LOGARITMOS:

Dados a y b pertenecientes a los reales positivos y distintos de 1.

loga (x.y) = logax + logay loga (x:y) = logax - logay logaxn=n.logax  (n ∈ ℜ) logax= logbx -------- logba loga1=0  ( ∀ a) logaa=1  ( ∀ a)

DEFINICIÓN DE LOGARITMO

y=logax  ⇔  ay=x

a > 0; a 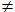1

X ∈ ℜ⁺

n ∈ ℜ

A continuación resolveremos ecuaciones logarítmicas con distintos niveles de complejidad:

1) log₂x=3

Resolvemos aplicando la definición

2) log₆(8 - 3x)=1

Para resolverlo, podemos utilizar la propiedad log_aa=1   ( ∀ a).

con lo cual (8 - 3x)=6, para que se cumpla log₆6=1.

3) 4log₃(2x - 5)=log₃81

Una de las formas para resolver este ejercicio es la siguiente:

Aplicando la propiedad log_axⁿ=n.log_ax  (n ∈ ℜ)

4log₃(2x - 5)=log₃81

log₃(2x - 5)⁴=log₃81

Para que esta igualdad se cumpla, entonces (2x - 5)⁴=81

(2x - 5)⁴=81

2x - 5 =⁴√81

2x - 5 =3

2x =3 + 5

2x =8

x =8/2

x=4

4) log₉(x + 1) + log₉9(x + 1) = 2

Por propiedad log_a(x.y) = log_ax + log_ay:

log₉( x + 1 ).9( x + 1) = 2

log₉9( x + 1 )² = 2

Aquí aplicaremos la definición de logaritmo:

9²=9 ( x + 1 )²

81 =9( x + 1 )²

81:9 =( x + 1 )²

9 =( x + 1 )²

√9 =| x + 1 |

3 =| x + 1 |

| x + 1 | = 3

x + 1 = 3 → x = 3 - 1 → x = 2 x + 1 = -3 → x = -3 - 1 → x = -4 Se anula, porque al reemplazar este valor en: log9( x + 1 ) + log99( x + 1 ) = 2 log9( - 4 + 1 ) + log99( - 4 + 1 ) = 2 log9( - 3 ) + log99( - 3 ) = 2 El argumento (-3), no puede ser negativo.

Por lo tanto, la respuesta es x=2

5) log²₂x - 5log₂x + 4 = 0

log²₂x - 5 log₂x + 4 = 0

Sustituimos log₂x = y

y² - 5y + 4 = 0

Calculamos mediante la fórmula resolvente los posibles valores de y:

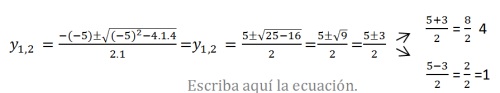
y₁= 4
y₂= 1

Debido a que habíamos sustituido log²x = y:

Para y1= 4 :		Para y1= 1 :
log2x = 4		log2x = 1
24 = x		21 = x
x1=16		x1=2