VOLVER A LOS ARTÍCULOS
Dado un número real a>0 y a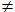
1, el logaritmo con base a de un número b es el exponente al que hay que elevar a la base a para obtener b y se representa de esta manera: Logab
Simbólicamente lo anterior se puede representar así: Logab = c ↔ ac = b
Veamos tres ejemplos:
Log5125 = 3 ya que 53 = 125
Log48 = 1.5 ya que 41.5 = 8
Log21 = 0 ya que 20 = 1
Nota: Para que la definición sea válida, no todas las bases y números son posibles. La base a tiene que ser positiva y distinta de 1, luego a > 0 y a 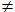1, b tiene que ser un número positivo b > 0 y c puede ser cualquier número real (c ∈ ℜ).
TIPS
No existen logaritmos de un número con base negativa:
∄ log-ab
No existen logaritmos de un número negativo:
∄ loga-b
No existe logaritmo de cero:
∄ loga0
El logaritmo de 1 es cero:
loga1= 0
El logaritmo en base a, de a es 1:
logaa= 1
El logaritmo en base de a, de una potencia en base de a, es igual a su exponente:
logaab= b
Propiedades de los logaritmos:
El logaritmo de un producto es igual a la suma de los logaritmos de los factores:
loga(x * y)= logax + logay
El logaritmo de un cociente es igual al logaritmo del dividendo, menos el logaritmo del divisor:
loga(x / y)= logax - logay
El logaritmo de una potencia es igual al producto del exponente, por el logaritmo de la base:
logaxn= nlogax
El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:
logan√x= 1/nlogax
Logaritmo decimal: son aquellos que tienen como base el número 10, comúnmente se representa por:
log10x= log(x)
Logaritmo neperiano:son aquellos que tienen como base el numero e, comúnmente se representa por:
logex= ln(x)
