Recta numérica

Es una línea recta en la cual se ubican los números reales. Cada número real tiene su posición sobre la recta y a cada punto de la recta le corresponde un número real.

Para graficar una recta numérica, se debe elegir un punto de referencia arbitrariamente, que representa el cero u origen.

Luego se coloca un signo + en un extremo y un signo - en el otro, para indicar el sentido positivo y negativo respectivamente.

El siguiente paso es seleccionar una escala para cada unidad. Por ejemplo, de un centímetro entre el 0 y el 1, manteniendo esta distancia entre dos enteros consecutivos que se coloquen en la recta.

Si por ejemplo, deseas marcar el punto -2 en la recta numérica anteriormente graficada, lo realizarás así:

¿Cómo ubicar decimales en la recta numérica?

Una vez que sabes ubicar los enteros en la recta, puedes continuar aprendiendo a colocar los decimales. Si por ejemplo, se desea colocar el número 0,6 en la recta, se debe dividir a la unidad en 10 partes. Una vez hecho esto, partiendo del cero, se cuentan 6 partes y en esa ubicación se encuentra el 0,6.

De igual modo para cualquier decimal que se desee colocar. En caso de ser 1,5; se debe realizar la división entre 1 y 2 para poder ubicarlo donde corresponda. O también, sabiendo que 1,5 se encuentra ubicado en el punto medio entre 1 y 2 nos queda:

Esto ocurre porque todos los números cuyas décimas son 5 (por ejemplo: 1,5; 2,5; -2,5) se ubican en el punto medio entre los dos números enteros consecutivos, anterior y posterior al número dado.

Los decimales se ubican en los espacios que existen entre los números enteros. Podemos colocar decimales no periódicos, decimales periódicos y también irracionales. Entre todos se completan todos los puntos de la recta numérica.

Los decimales pueden expresarse en forma de fracción, lo cual es muy útil al momento de graficar aquellos que son periódicos.

¿Cómo ubicar fracciones en la recta numerica?

Para ubicar una fracción en la recta numérica, se procede a dividir el entero, tantas veces como lo indique su denominador.

Ejemplo: 2/3

Si el numerador es mayor que el denominador, es necesario seguir dividiendo en partes a la unidad consecutiva. Observa el siguiente ejemplo:

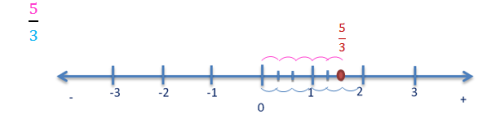
No alcanza con dividir una unidad, porque como debemos tomar 5 partes, nos faltan 2. Por ello se repite la división en partes entre el 1 y el 2.

Este mismo procedimiento se realiza también con fracciones negativas.