VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
La porción de plano comprendida entre dos semirrectas es denominada ángulo, teniendo este un origen, O, común, llamado vértice y las dos semirrectas reciben el nombre de lados del ángulo.
Los ángulos se denominan mediante tres letras mayúsculas, una para el origen y las otras dos para los lados, ejemplo: 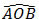 .
.
Para realizar la medida de un ángulo, se utiliza un instrumento llamado semicírculo graduado o transportador de ángulos, usualmente éste da la medida de los ángulos en grados sexagesimales o grados centígrados. Cada grado corresponden a 1/360 parte de una circunferencia completa, la cual abarca por tanto 360 grados, o 360º.
Clasificación de ángulos de acuerdo a su amplitud
Este ángulo se forma por dos semirrectas con amplitud mayor de 0 grados y menor de 90º.

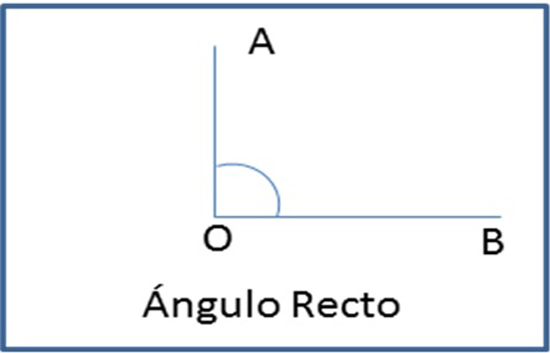
Un ángulo recto tiene una amplitud igual 90º sexagesimales.
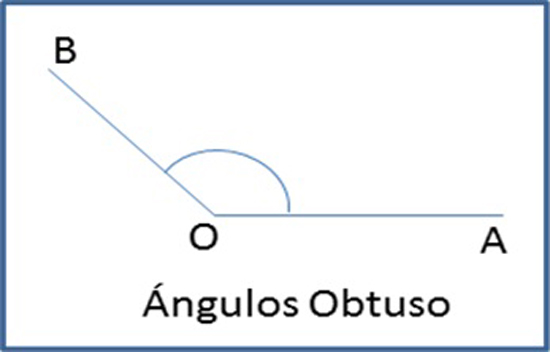
Un ángulo obtuso es aquel cuya amplitud es mayor a π/2 rad y menor a π rad, es decir mayor a 90º y menor a 180º sexagesimales.
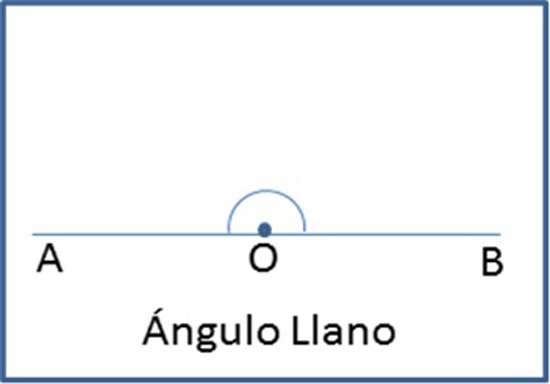
Este ángulo posee una amplitud de π rad o 180º.
Un ángulo completo es aquel que mide 360º o 2π rad.

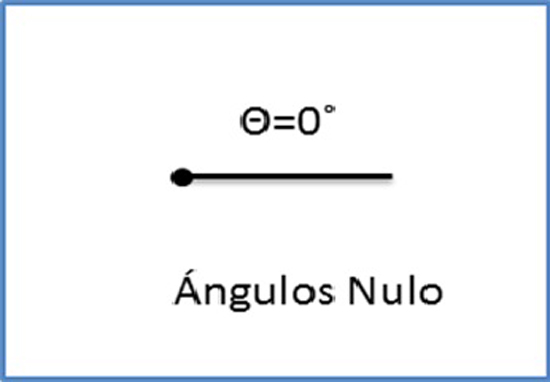
Un ángulo nulo es aquel cuya amplitud es de 0º.
Un ángulo convexo tiene una amplitud mayor que 0º y menor que 180º.

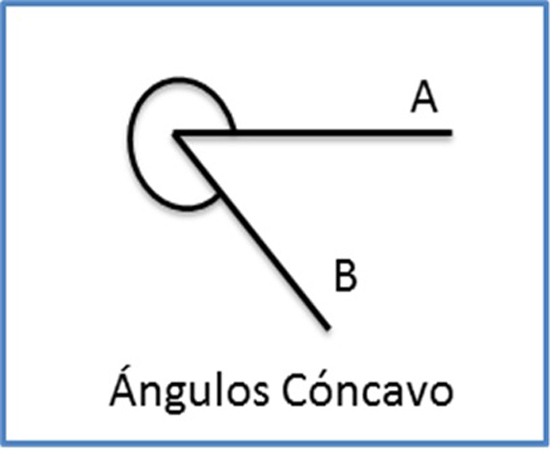
Un ángulo cóncavo lleva una amplitud mayor que 180º.
Ángulos relacionados según su posición
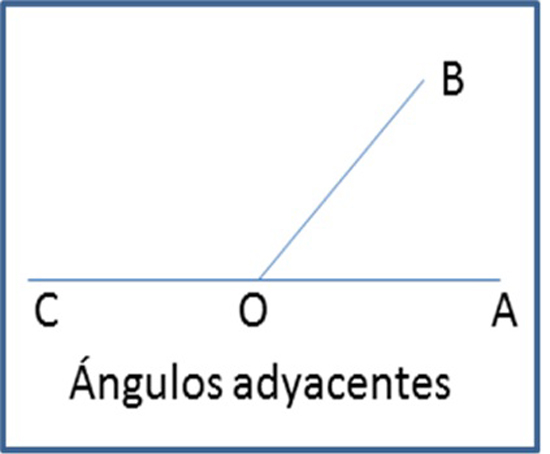
Este tipo de ángulos tienen un vértice y un lado común, y los otros lados restantes situados en prolongación uno con el otro, no tienen ningún punto interior común.
Estos tienen un lado y el vértice común.
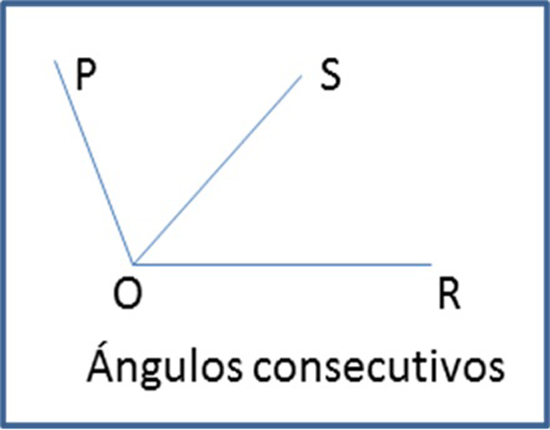
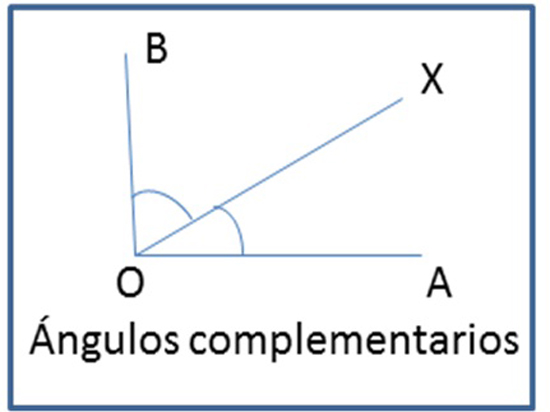
Son ángulos cuya suma de medidas es π/2 radianes o 90º.
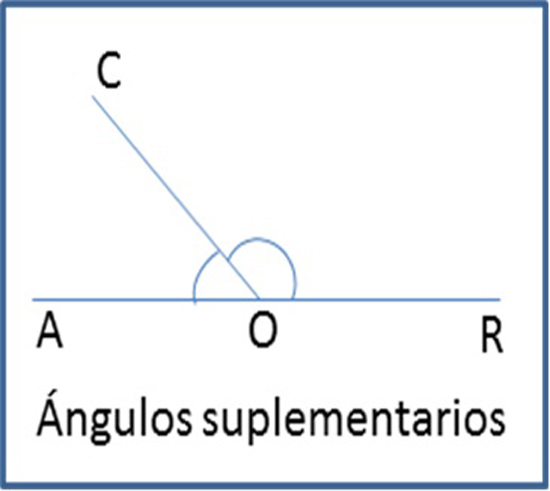
Aquellos cuya suma de medidas es π radianes o 180º.
Son los que teniendo el vértice común, los lados de uno son prolongación de los lados del otro, es decir, dos ángulos se dicen opuestos por el vértice cuando los lados de uno son semirrectas opuestas a los lados del otro.

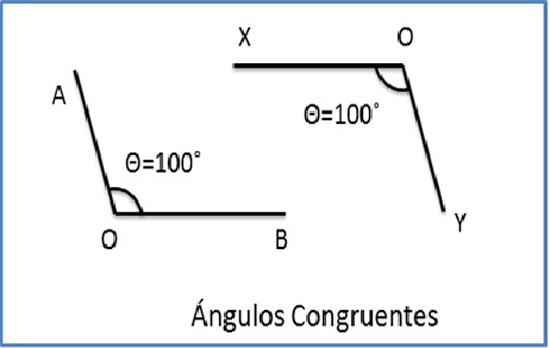
Ángulos congruentes
Aquellos que tienen la misma amplitud, es decir, que miden lo mismo.
Ángulos resultantes de dos rectas paralelas y una transversal
Dos rectas cualesquiera cortadas por una tercera determinan ocho ángulos. De acuerdo a la ubicación de los ángulos se clasifican en:
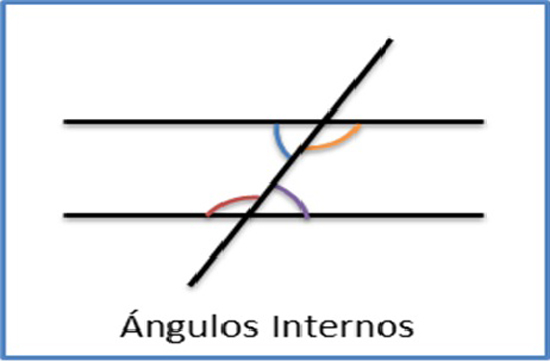
Los ángulos ubicados en la zona comprendida entre las rectas paralelas se llaman ángulos interiores.
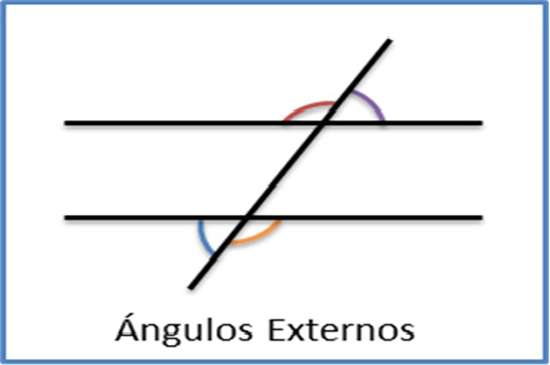
Los ángulos que caen fuera del espacio entre las dos rectas, los ángulos que no son interiores, se llaman ángulos exteriores.
En dos rectas cortadas por una transversal, son ángulos correspondientes los que están del mismo lado de la transversal pero uno es interno y el otro externo a las dos rectas, además, las dos rectas son paralelas si y solo si, los ángulos correspondientes son congruentes.
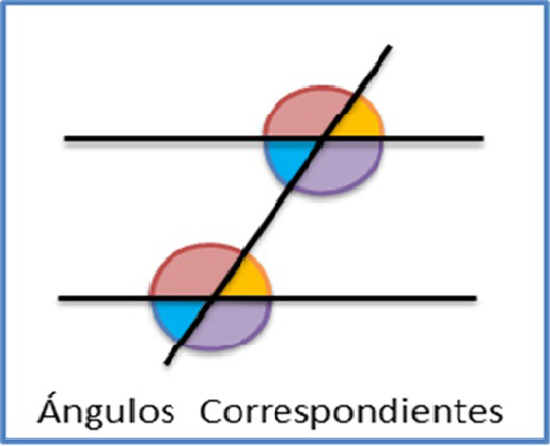
Los ángulos denotados con el mismo color,
son los correspondientes.
Si dos ángulos están situados en distintos semiplanos con respecto a la transversal y ambos son internos, se los llama ángulos alternos internos. Los ángulos alternos internos entre paralelas son iguales, asimismo, si dos rectas cortadas por una tercera forman ángulos alternos internos iguales, las rectas son paralelas.

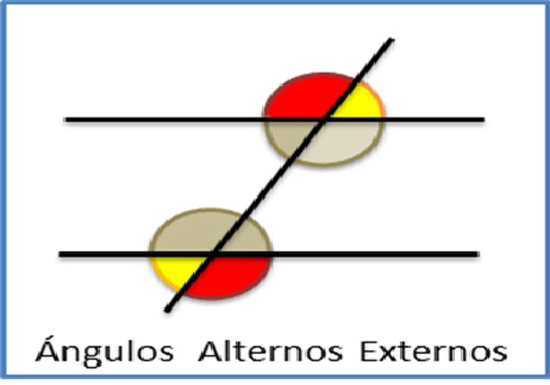
Si dos ángulos están situados en distintos semiplanos con respecto a la transversal y ambos son externos, se los llama ángulos alternos externos. Los ángulos alternos externos entre paralelas son iguales, de este modo, si dos rectas cortadas por una tercera forman ángulos alternos externos iguales, las rectas son paralelas.
Si dos ángulos están situados en un mismo semiplano con respecto a la transversal y ambos son internos, se los llama ángulos conjugados internos. Los ángulos conjugados internos entre paralelas son suplementarios. Asimismo, si dos rectas cortadas por una tercera forman ángulos conjugados internos suplementarios, las rectas son paralelas.
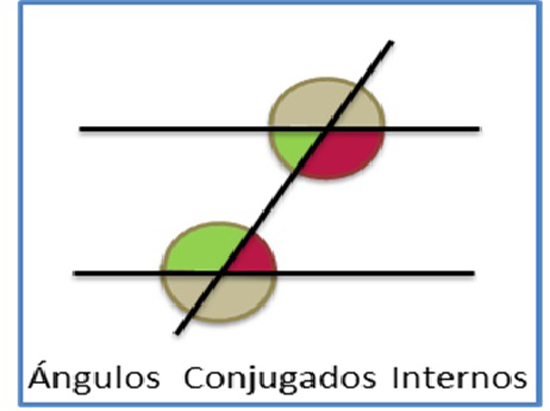
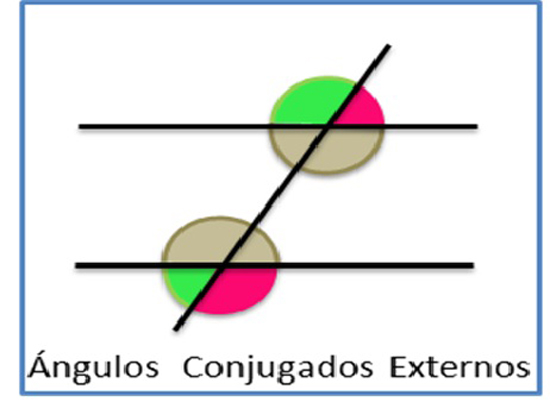
Si dos ángulos están situados en un mismo semiplano con respecto a la transversal y ambos son externos, se los llama ángulos conjugados externos. Los ángulos conjugados internos entre paralelas son suplementarios. De igual modo, si dos rectas cortadas por una tercera forman ángulos conjugados internos suplementarios, las rectas son paralelas.