 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS
Para realizar problemas o ejercicios que soliciten el cálculo de áreas sombreadas, se deben recordar las fórmulas de las áreas de las distintas figuras geométricas, triángulo, cuadriláteros, círculo y polígonos. Si deseas revisar dichas fórmulas puedes ingresar en el Tomo de Geometría de la Enciclopedia de Matemática Secundaria.
Los pasos a seguir en la realización de este tipo de ejercicios son los siguientes:
1) Identificar en qué figuras geométricas puede descomponerse la figura dada.
2) Escribir las fórmulas de las figuras que intervienen.
3) Colocar los datos que aporta el ejercicio o problema.
4) Realizar equivalencias entre unidades si es necesario, todos los lados deben estar expresados en la misma unidad, por ejemplo, todos en cm.
5) Calcular las áreas de cada figura y luego realizar restas o sumas, de acuerdo a lo que se necesite hallar.
En el siguiente ejemplo, se desarrollará cada uno de los pasos.
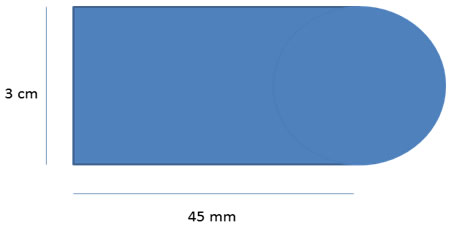
Hallar el área de la parte sombreada de la siguiente figura:

1) Identificar en qué figuras geométricas puede descomponerse la figura dada:
En este caso, se observa un rectángulo y un medio círculo.

2) Fórmulas:
Área rectángulo: A= b.h
Área semicírculo: A= π.r²:2
3) Datos:
h= 3 cm → d= 3 cm d: diámetro del círculo
b= 45 mm
4) La altura está expresada en cm y la base en mm, por lo tanto debemos realizar una equivalencia para obtener unidades iguales.
10 mm ------------------- 1 cm
45 mm ------------------- 4,5 cm
Se trabajará entonces con los siguientes datos:
h= 3 cm → d= 3 cm d: diámetro del círculo
b= 4,5 cm
5) Cálculo de áreas por separado:
Área del rectángulo: A= b.h = 4,5 cm . 3 cm = 13,5 cm²
Área del semicírculo: A= 3,1416.(1,5 cm)² :2= 3,5343 cm²

En este caso se le debe quitar un semicírculo al rectángulo, por ello se debe realizar la operación de resta.
Área sombreada = Área del rectángulo – Área del semicírculo
Área sombreada = 13,5 cm²- 3,5343 cm²= 9,9657 cm²
Por lo tanto, el área sombreada de la figura es 9,9657 cm².
También es posible que en vez de restar, sea necesario sumar, un ejemplo de figura en la cual se debería sumar, es la siguiente:
En este caso, el semicírculo, debería ser sumado.
De este modo, se puede hallar cualquier área solicitada, que puede componerse por dos o más figuras geométricas.