Cuerpos redondos. Áreas y volúmenes.

---

Son cuerpos geométricos que están limitados por superficies curvas en parte o en su totalidad. Entre ellos se encuentran el cilindro, el cono y la esfera.

Cuerpos redondos en la vida cotidiana:

Sombrero asiático de bambú.

Helado.

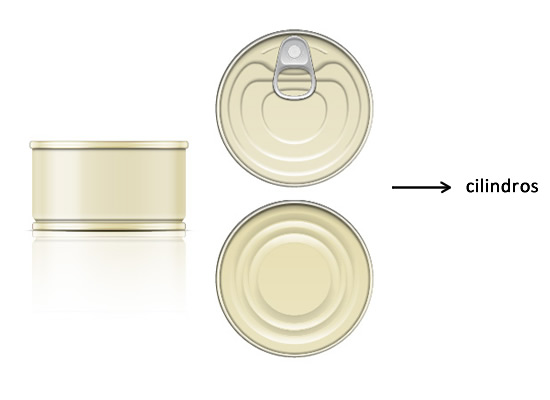
Latas de conservas.

Mira a tu alrededor y podrás ver muchos cuerpos redondos, pelotas, frutas como la naranja, adornos, recipientes, monedas, etc.

Los cuerpos redondos también son denominados cuerpos de revolución, debido a que se originan al girar una figura plana alrededor de un eje fijo.

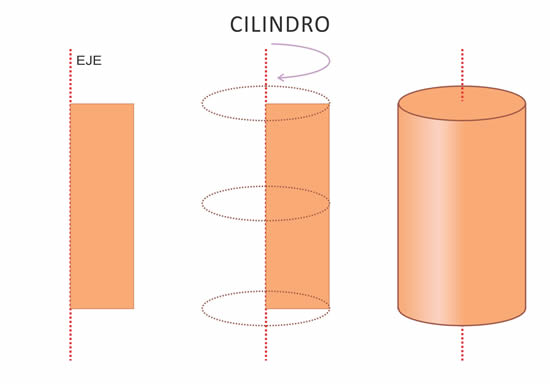
CILINDRO

El cilindro se genera al girar un rectángulo sobre uno de sus lados. Los elementos del cilindro son los siguientes:

• Eje.
• Bases.
• Altura.
• Generatriz.
• Radio.

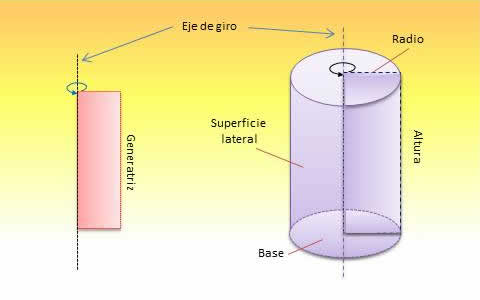
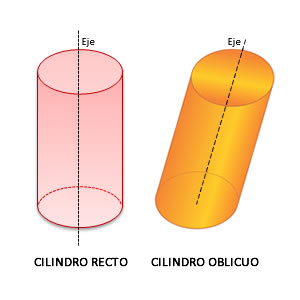
El eje, es la recta que contiene al lado fijo del rectángulo. Cuando el eje es perpendicular a las bases, el cilindro es recto; si el eje es oblicuo a las bases el cilindro es oblicuo.

Las bases, son los círculos paralelos que se generan al girar el rectángulo. Éstas son congruentes (iguales).

La altura (h), corresponde al segmento que une a los centros de las bases.

La generatriz (g), , es el lado del rectángulo que al girar genera la superficie lateral del cilindro.

El radio (r), , de la base es la mitad del diámetro de cada uno de los círculos que forman sus bases.

DESARROLLO DEL CILINDRO

El desarrollo de un cuerpo geométrico consiste en representarlo en un plano. A continuación se puede observar cómo se obtiene el desarrollo de un cilindro recto:

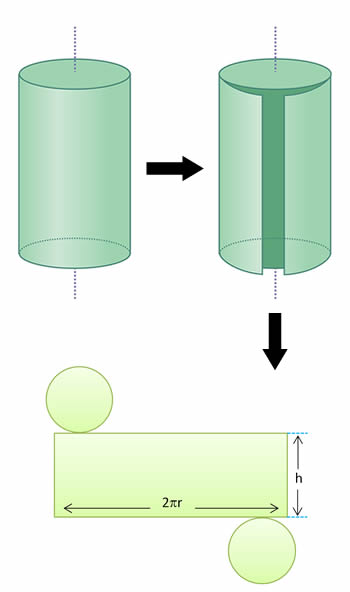
Área y volumen de un cilindro

Al observar el desarrollo del cilindro, se puede notar que el área lateral es la de un rectángulo que tiene como base la longitud de la circunferencia y como altura, la altura o generatriz del cilindro.

CILINDRO
Área lateral	A l = 2 · π · r · h
Área total	AT = A l + 2 · AB
Volumen	V = AB · h

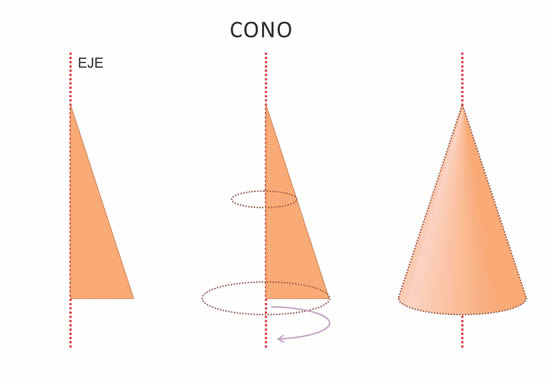
CONO

El cono es el cuerpo geométrico de revolución que se obtiene al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.

Elementos del cono

• Eje: Es el cateto fijo alrededor del cual gira el triángulo.
• Base: Es el círculo que forma el otro cateto.
• Altura (h): Es el segmento que une el vértice y el centro de la base.
• Radio (r): es el radio del círculo que forma la base.
• Generatriz (g): es el segmento que genera el cono, es decir, es la hipotenusa del triángulo rectángulo, ya que la altura, el radio de la base y la generatriz forman un triángulo rectángulo.

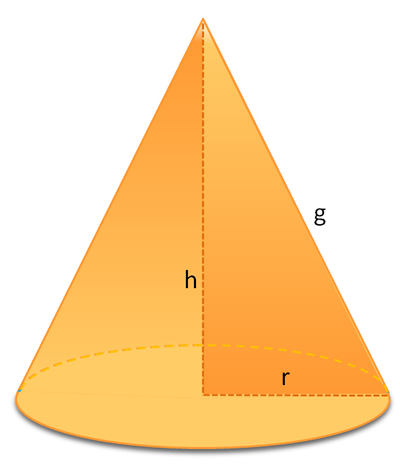
DESARROLLO DEL CONO

Área y volumen del cono

El área total de un cono se obtiene al sumar el área de la base, que es un círculo más el área lateral, que está dada por la expresión π.r.g.

CONO
Área lateral	A l = π · r · g
Área total	AT = A l + AB
Volumen	V = (AB · h) / 3

El área de la base del cono (A_B) es π.r², por lo tanto, el volumen también se puede expresar como:

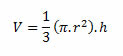
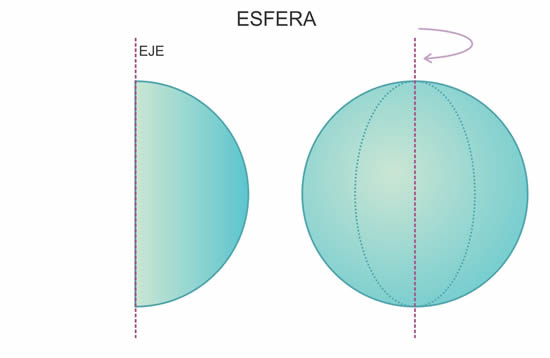
ESFERA

Una esfera es un semicírculo que gira sobre su diámetro y que describe en el espacio un cuerpo redondo.

Si consideramos una semicircunferencia que gira sobre su diámetro, la superficie curva que se genera es la superficie esférica.

Elementos de la Esfera

• Centro: Punto interior que equidista de cualquier punto de la superficie de la esfera, justamente es el mismo centro del círculo.
• Radio: es la distancia del centro a un punto de la superficie de la esfera, siendo cualquier segmento que une el centro con cualquier punto de la superficie.
• Cuerda: Segmento que une dos puntos de la superficie esférica.
• Diámetro: Cuerda que pasa por el centro.
• Polos: Son los puntos de intersección del eje de giro con la superficie esférica.

Área y volumen de la esfera

Área de la superficie esférica:

A = 4πr²

Volumen de la esfera:

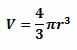
A continuación, un útil resumen de fórmulas: