 VOLVER A LOS ARTÍCULOS
VOLVER A LOS ARTÍCULOS

Cuando escuchas la palabra inecuación ¿con qué la relacionas? ¿Con ecuación? Ocurre esto porque ambas son expresiones algebraicas que contienen incógnitas. Pero la diferencia está en que en la ecuación se establece una expresión de igualdad, y en la inecuación, de desigualdad.
Que no te asusten los términos matemáticos ni la teoría. Veamos dos casos prácticos para entender de qué estamos hablando.
A ver si sabes: ¿Cuánto dinero llevó María al almacén si gastó $8 y le dieron $2 de vuelto?
Este problema se puede expresar en forma de ecuación. Sería así: x – 8 = 2 La x representa la cantidad de dinero que llevó María y es lo que debemos averiguar; 8 es lo que gastó de ese dinero; y 2, lo que le devolvieron.
Entonces: x – 8 = 2  x = 8+2
x = 8+2  x = 10 Rta: María llevó $10 al almacén.
x = 10 Rta: María llevó $10 al almacén.
En este caso ocurre que existe una sola respuesta a la pregunta, es decir, la variable x solo puede tener una solución. Pero determinados problemas no se resuelven calculando un único valor de una magnitud, sino que su respuesta exige determinar toda una colección de valores de dicha magnitud, los cuales deben cumplir una condición determinada.
A ver si sabes: Dentro de cuatro años, María tendrá más de veintiséis años. ¿Qué edad tiene actualmente María?

En primera instancia, se representa a la edad actual de María con la letra x, para poder escribir en lenguaje matemático el enunciado. La edad de María dentro de cuatro años es x+4. Entonces nos quedaría expresado de la siguiente manera:
x+4>26
Se despeja de forma similar a una ecuación, pasamos el +4 al lado derecho de la desigualdad, como un -4:
x>26-4
x>22
Obtenemos entonces la solución. Como x es mayor (>) que veintidós, podemos decir que María puede tener en la actualidad 23, 24, 25, 26 o más años. María tiene 23 años como mínimo.
En ocasiones se utiliza el símbolo ≥, en ese caso incluiría el primer valor obtenido, por ejemplo, si el problema estuviese planteado así:
Dentro de cuatro años, María tendrá veintiséis años o más. ¿Qué edad tiene actualmente María?
Aquí el 26 está incluido, por lo tanto se coloca ≥, así:
x+4 ≥ 26
x ≥ 22
Por lo tanto, María actualmente tiene 22 años como mínimo.
SÍMBOLOS DE DESIGUALDAD
En las Inecuaciones los símbolos que representan la desigualdad son:

Las inecuaciones nos dan como resultado un conjunto de valores en el cual la variable puede tomar un valor cualquiera de ese conjunto. Tal conjunto, que se puede expresar como intervalo, constituye la solución general de la inecuación.
PROPIEDADES DE LAS DESIGUALDADES
Para calcular los valores que integran el conjunto solución se debe transformar la inecuación, de forma similar a cómo se hace para una ecuación, teniendo en cuenta las siguientes propiedades de las desigualdades:
• Al sumar o restar un mismo número a los dos miembros de una desigualdad o inecuación, el resultado es otra desigualdad del mismo sentido o equivalente a la primera, por ejemplo:
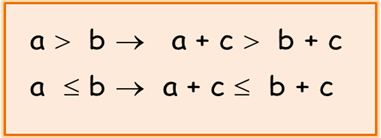
a,b y c son números positivos, c es distinto de cero.
En una desigualdad un término cualquiera puede pasar de un miembro a otro cambiándole el signo, si está con signo positivo pasa a negativo, y si está con signo negativo pasa a positivo. Por ejemplo: en la desigualdad, a + c > b, podemos pasar c al segundo miembro con signo negativo quedando, a > b – c, lo que es equivalente de restar c en ambos miembros.
• Al multiplicar o dividir los dos miembros de una inecuación por un número positivo, la inecuación resultante es equivalente a la dada y su símbolo no varía, por ejemplo:
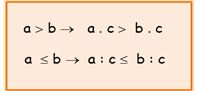
a,b y c son números positivos, c es distinto de cero.
• Al multiplicar o dividir los dos miembros de una desigualdad por un mismo número negativo, la desigualdad cambia de sentido, es decir, su símbolo varía, así:
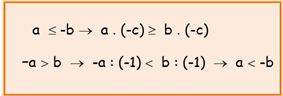
a,b y c son números positivos en este cuadro.
Es decir, al cambiar todos los signos de una desigualdad, el símbolo de esta también varía, porque equivale a multiplicar los dos miembros de la inecuación por -1. Por ejemplo, si tenemos a – b > -c, cambiando los signos o multiplicando por -1, obtenemos: -a + b < c.
• Si cambia el orden de los miembros, entonces el símbolo de la desigualdad también cambia de sentido.

• Si se invierten ambos miembros de la desigualdad, el símbolo de la misma también deberá ser cambiado.
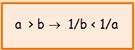
¿CÓMO RESOLVER UNA INECUACIÓN?
Es necesario ir transformando la inecuación inicial en otras equivalentes más simples hasta que el resultado final sea tal que se conozca el intervalo solución, o hasta que el resultado final sea contradictorio, en cuyo caso, la inecuación no tiene solución.
En general las soluciones se pueden expresar así:
• Una representación gráfica.
• Un intervalo: conjunto de números reales que satisfacen la ecuación.
Una inecuación de primer grado es aquella en la que sus dos miembros son polinomios de grado menor o igual a 1, debiendo tener al menos uno de ellos grado 1. Las soluciones de una inecuación son todos los números reales que hacen que dicha inecuación sea verdadera.
Para resolver inecuaciones que contengan una incógnita y ésta tenga como exponente mayor el número 1, se pueden seguir los siguientes pasos:
¿Qué edad tiene Ximena si cuando al doble de su edad se le restan 17 años, se obtiene un resultado menor que 35 y cuando a la mitad de su edad se le suma 3, se obtiene un resultado mayor que 15?
2x – 17 < 35 x/2 + 3 > 15
2x < 35 + 17 x/2 > 15 - 3
2x < 52 x > 12 . 2
x < 52 : 2 x> 24
x < 26
Respuesta: 24 < x < 26  Ximena tiene 25 años.
Ximena tiene 25 años.