Expresiones algebraicas

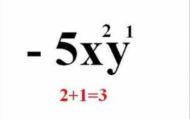
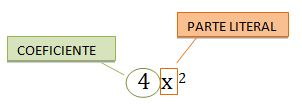
Parte Literal: Las letras son las incógnitas, es decir, las cantidades desconocidas o indeterminadas. También se las denomina variables.

Coeficientes: Son los números, corresponden a valores constantes que acompañan a las variables.

MONOMIO: Es una expresión algebraica compuesta por un solo término. Ejemplo:

7x³

BINOMIO: Es una expresión algebraica formada por dos términos. Ejemplo:

2x² + x

Siguiendo este razonamiento, el trinomio está compuesto por tres términos y el cuatrinomio por cuatro.

POLINOMIO: Un polinomio es una expresión algebraica formada por una suma de términos de la forma axⁿ. Siendo a ∈ R y n ∈ N₀. Ejemplo:

P(x) = 9x⁷ + 4x³ + 2² - x + 1

Grado de un polinomio: El grado de un polinomio es el mayor exponente al cual está elevada la variable x.

Coeficiente principal: Es el número que acompaña a la incógnita que tiene el exponente mayor.

Término independiente: Es el término numérico que no está acompañado de parte literal.

¿Cómo hallar el valor numérico de una expresión algebraica?

El valor numérico de una expresión algebraica se obtiene reemplazando todas las letras por números y luego resolviendo las operaciones indicadas.

Reemplazamos por los valores correspondientes:

4 · 5 = 20 + 2 = 22

Recuerda colocar paréntesis cuando tenemos que sustituir una letra por un número negativo. Esto se hace para no cometer errores con la regla de los signos en los cálculos posteriores. Por ejemplo:

2x + 4z; si x = 2 y z = -1

2 · 2 + 4 · (-1) = 4 - 4 = 0

Operaciones con expresiones algebraicas

Veamos varios ejemplos que nos ayudarán a comprender como realizar este tipo de operaciones.

OPERACIONES CON MONOMIOS

Suma de monomios de igual grado:

4x⁵ + 2x⁵ = 6x⁵

Se suman los coeficientes y se coloca la misma parte literal con su exponente.

Esto ocurre porque se ha hecho mentalmente: factor común. (4+2)x⁵ = 6x⁵

Suma de monomios de distinto grado:

2x + 3x² = 2x + 3x²

Queda igual porque si los monomios no tienen el mismo exponente no dan como resultado otro monomio.

Resta de monomios: Se opera de manera similar a la suma.

Resta de monomios de igual grado:

10x² - 6x² = 4x²

Resta de monomios de distinto grado:

4x³ - x = 4x³ - x

Multiplicación de monomios:

2x⁷.5x³ = 10x¹⁰ Se multiplican los coeficientes y se suman los exponentes.

División de monomios:

25x⁵:5x² = 5x³ Se dividen los coeficientes y se restan los exponentes.

OPERACIONES CON POLINOMIOS

Binomios, trinomios y cuatrinomios son casos particulares de polinomios. Es decir, están incluidos dentro de éstos últimos.

Si profundizamos un poco más, diremos que un monomio también es un polinomio, pero eso ya lo veremos en detalle más adelante.

Vamos a ejercitar un poco más:

Multiplicación de un monomio por un binomio:

5x.(4x - 1) = 20x² - 5x Se realiza la propiedad distributiva.

Multiplicación de dos binomios:

(2x + 6)(x - 2)=2x² - 4x + 6x - 12 = 2x² + 2x - 12

Distribuimos y luego sumamos aquellos términos que tienen variables con el mismo grado. En este caso -4x + 6x.

División de un binomio por un monomio:

(10x² + 5x):5x = 2x +1

Suma de polinomios:

(3x³ - x² + x + 1)+(9x⁴ + 2x² + 3) = 9x⁴ + 3x³ + x² + x + 4

Se suman aquellos términos que tienen iguales exponentes.

Resta de polinomios:

(4x⁵ - 3x² + 2x) - (2x⁴ +3x³ - 5x +3) = 4x⁵ - 3x³ + 2x - 2x⁴ - 3x³ + 5x - 3 = 4x⁵ - 2x⁴ - 6x³ + 7x - 3

Multiplicación de polinomios:

(x³ + 2x + 1)(x + 5) = x⁴ + 5x³ + 2x² + 10x + x + 5 = x⁴ + 5x³ + 2x² + 11x + 5

Además de las operaciones algebraicas anteriormente vistas, que contienen a la x como incógnita, podemos encontrar expresiones algebraicas con otra parte literal. Veamos algunos ejemplos:

1) 3ab + 2ab = (3 + 2)ab = 5ab

2) 2ac.3bc = 2.3.a.b.c.c = 6abc²

3) 2a - 2ab = 2a(1-b)

4) xyz + xy + y² = y (xz + x + y)

5) (4abc⁴)/(2ac) = (4/2)bc² - 1 = 2bc³

Cómo vemos en los ejercicios previos, las letras pueden ser distintas a la x o podemos trabajar con más de una incógnita en el mismo ejercicio.

Algunas consideraciones al trabajar con más de una incógnita, son las siguientes:

• Para sumar o restar se realiza factor común, si es posible hacerlo.
• Al multiplicar, se multiplican los coeficientes y se suman los exponentes de las partes literales iguales.
• Al dividir, se dividen los coeficientes y se restan los exponentes de partes literales iguales.
• Las expresiones algebraicas, deben escribirse colocando primero la parte numérica y luego las letras por orden alfabético.
• No es necesario colocar un punto entre coeficiente y parte literal o entre dos partes literales, se sobreentiende que en ese caso están multiplicándose.

Puedes continuar estudiando el tema con el artículo: Casos de factoreo, si así lo deseas.