Producto vectorial de Gibbs

En el producto vectorial, como su nombre lo indica, intervienen vectores. También es conocido como producto cruz y tiene variadas aplicaciones, tanto en matemática como en física e ingeniería.

Dados tres vectores $\vec{u}, \vec{v} y \vec{w}$ , existen tres clases de multiplicación que pueden efectuarse utilizando algunos o todos ellos:

Producto escalar
$\vec{u} \cdot \vec{v}, \vec{u} \cdot \vec{w}, \vec{v} \cdot \vec{w}$
Producto vectorial
$\vec{u} x \vec{v}, \vec{u} x \vec{w}, \vec{v} x \vec{w}$
Producto mixto
$\vec{v} \cdot (\vec{u} x \vec{w}), \vec{w} \cdot (\vec{u} x \vec{v}), \vec{u} \cdot (\vec{v} x \vec{w})$

En el caso 1 y 3 el resultado es siempre un escalar, pero en el caso 2 el resultado de dicha operación es siempre un nuevo vector, $\vec{r}$ .

En esta oportunidad se estudiará el producto vectorial (caso 2). Se sabe que el resultado es un vector y por lo tanto tiene su propia dirección, sentido y modulo. Si los vectores a multiplicar son , para hacer el producto vectorial sería .

producto vectorial

Características

La dirección del vector resultante es siempre perpendicular al plano que forman los vectores . Es decir:.

VECTORES PERPENDICULARES

Cuando dos vectores son perpendiculares (ortogonales) su producto escalar es igual a cero.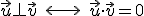

El sentido del vector resultante se obtiene al usar la “regla de la mano derecha”, la cual nos dice que si se abarca el menor ángulo entre $\vec{u}y\vec{v}$ con los dedos índice y anular, el pulgar indica el sentido de $\vec{r}$ .

Regla de la mano derecha, se puede utilizar para determinar sentidos y direcciones vectoriales.

El modulo del vector resultante es el área del paralelogramo que forman los vectores y se calcula con la siguiente fórmula:
$|\vec{r}| = |\vec{u}| \cdot |\vec{v}| \cdot s e n α$ Siendo α el ángulo comprendido entre .

Cálculo analítico del producto vectorial

Dados dos vectores:

$\vec{i},\vec{j},\vec{k}$ son versores ubicados en los ejes x, y, z respectivamente.

Versor: vector unitario con módulo igual a uno.

Componentes de un vector

$\fn_cm \small _{u_{x}},_{u_{y}},_{u_{z}}$ son las componentes del vector $\fn_cm \small \vec{u}$ .

$\fn_cm \small _{v_{x}},_{v_{y}},_{v_{z}}$ son las componentes del vector $\fn_cm \small \vec{v}$ .

Vector expresado en sus componentes x, y, z

Imagen realizada con calculadora gráfica 3D, Geogebra.

Se calcula el producto vectorial de la siguiente manera:

Se forma una matriz 3×3, en la cual la primera fila corresponde a los versores unitarios $\vec{i}, \vec{j}, \vec{k}$ . En la segunda fila se colocan las componentes del primer vector y en la tercera fila se ubican las componentes del último vector.

Se aplica la regla de Sarrus (método para matrices de 3×3) para hallar el determinante de la matriz:

“En el producto vectorial el orden de los factores sí afecta el producto. Es decir que $\fn_cm \small \vec{u}x\vec{v}\neq \vec{v}x\vec{u}$ “.

Ejemplo 1:

Dados dos vectores:

Estos dos vectores se pueden reescribir en sus coordenadas:

Se conforma una matriz 3×3:

Luego se procede a aplicar la fórmula, teniendo en cuenta que cada matriz 2×2 se conforma de la siguiente forma:

Se resuelven las matrices. Observar que los términos con signo + corresponden a los productos de las multiplicaciones de las diagonales:

Y se restan los productos de las diagonales que tienen la siguiente dirección:

Se realizan las operaciones correspondientes:

De esta forma se obtiene el resultado del producto vectorial $\fn_cm \small \vec{u}x\vec{v}$ :

Ejemplo 2:

Utilizando los mismos vectores que en el ejemplo anterior se realizará el producto vectorial $\fn_cm \small \vec{v}x\vec{u}$ :

que puede expresarse como

En los ejemplos anteriores se ha visto un ejemplo sobre la propiedad que indica que el orden de los factores sí afecta al producto vectorial. En dichos ejemplos se observa:

≠

Observar que ambos vectores son distintos, uno es el opuesto del otro.

VECTORES OPUESTOS

Dos vectores opuestos son aquellos que tienen el mismo módulo y dirección, pero sentidos opuestos.

aplicaciones del PRODUCTO VECTORIAL EN FÍSICA

Velocidad tangencial en un momento circular:

Momento angular con respecto al origen:

Torque respecto a un origen:

Fuerza magnética sobre una carga:

A PRACTICAR LO APRENDIDO

RESPUESTAS

1. (-3, 3, 1)

2. (-3,7, -1)

3. (-1, 2, 3)

¿Sabías qué...?

Pierre Frédéric Sarrus estaba indeciso con respecto a qué estudios superiores realizar, se debatía entre Medicina y Matemáticas. Finalmente ingresó a Matemáticas porque no cumplió con los requisitos solicitados en 1815 para iniciar Medicina, dado que era protestante y bonapartista.